Câu hỏi:
2 năm trước
Cho 2 mạch điện như hình vẽ:
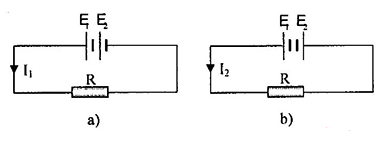
\({E_1} = 18V,{r_1} = 1\Omega \). Cho \(R = 9\Omega \), \({I_1} = 2,5A\), \({I_2} = 0,5A\). Tìm \({E_2}\) và \({r_2}\)
Trả lời bởi giáo viên
Đáp án đúng: b
Từ mạch điện a, ta thấy 2 nguồn đều là máy phát, nên ta có:
Cường độ dòng điện cho mạch kín: \({I_1} = \dfrac{{{E_b}}}{{R + {r_b}}} = \dfrac{{{E_1} + {E_2}}}{{R + {r_1} + {r_2}}}\)
\( \Leftrightarrow 2,5 = \dfrac{{18 + {E_2}}}{{9 + 1 + {r_2}}}\)
\( \Rightarrow 2,5\left( {10 + {r_2}} \right) = 18 + {E_2}\)
\( \Rightarrow {E_2} - 2,5{r_2} = 7\) (1)
Từ mạch điện b, ta thấy máy 1 là máy phát còn máy 2 là máy thu, nên định luật ôm viết cho mạch kín chứa máy phát và máy thu là: \({I_2} = \dfrac{{{E_1} - {E_2}}}{{R + {r_1} + {r_2}}}\)
\( \Leftrightarrow 0,5 = \dfrac{{18 - {E_2}}}{{9 + 1 + {r_2}}}\)
\( \Rightarrow 0,5\left( {10 + {r_2}} \right) = 18 - {E_2}\)
\( \Rightarrow {E_2} + 0,5{r_2} = 13\) (2)
Từ (1) và (2), ta có: \(\left\{ \begin{array}{l}{E_2} - 2,5{r_2} = 7\\{E_2} + 0,5{r_2} = 13\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{E_2} = 12V\\{r_2} = 2\Omega \end{array} \right.\)
Hướng dẫn giải:
+ Xác định máy phát, máy thu
+ Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{{{E_b}}}{{{R_N} + r}}\)
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
