Câu hỏi:
2 năm trước
Xe A chuyển động với vận tốc \(3,6km/h\) đến va chạm vào xe B đang đứng yên. Sau va chạm xe A dội ngược lại với vận tốc \(0,1m/s\), còn xe B chạy với vận tốc \(0,55m/s\). Biết ${m_B} = 200g$. Tìm ${m_A}$
Trả lời bởi giáo viên
Đáp án đúng: a
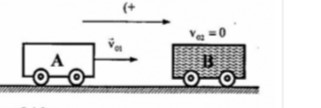
Chọn chiều dương là chiều chuyển động của ban đầu của xe A.
Áp dụng định luật III Niutơn cho tương tác của hai xe ta có:
\({m_1}\overrightarrow {{a_1}} = {m_2}\overrightarrow {{a_2}} \\\Leftrightarrow {m_1}\dfrac{{\overrightarrow {{v_1}} - \overrightarrow {{v_{01}}} }}{{\Delta t}} = - {m_2}\dfrac{{\overrightarrow {{v_2}} - \overrightarrow {{v_{02}}} }}{{\Delta t}}\)
Chiếu lên chiều dương đã chọn, ta được: \({m_A}\dfrac{{ - {v_1} - {v_{01}}}}{{\Delta t}} = - {m_B}\dfrac{{{v_2}}}{{\Delta t}}\)
\({m_A} = \dfrac{{{m_B}{v_2}}}{{{v_1} + {v_{01}}}} = \dfrac{{0,2.0,55}}{{0,1 + 1}} = 0,1kg\)
Vậy khối lượng của xe A là: \(0,1 kg\)
Hướng dẫn giải:
Vận dụng định luật II Niutơn: \(\overrightarrow F = m\overrightarrow a \)
