Với giao điểm \(A,B\) của\(\left( P \right)\) và \(d\) ở ý trước . Gọi \(C,D\) lần lượt là hình chiếu vuông góc của \(A,B\) lên \({\rm{Ox}}\). Tính diện tích tứ giác \({\rm{ABDC}}\).
Trả lời bởi giáo viên
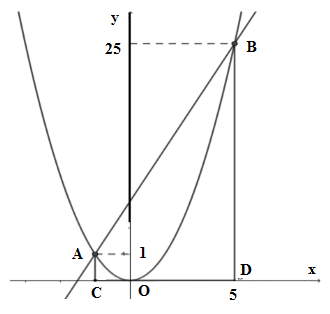
Ta có \(A\left( { - 1;1} \right);B\left( {5;25} \right)\) nên \(C\left( { - 1;0} \right);D\left( {5;0} \right)\)
\( \Rightarrow AC = \sqrt {{0^2} + {{\left( { - 1} \right)}^2}} = 1;\)\(DC = 6;BD = \sqrt {{0^2} + {{25}^2}} = 25\)
Vì \(AC \bot BC;BD \bot BC \Rightarrow ABDC\) là hình thang vuông nên \({S_{ABDC}} = \dfrac{{\left( {AC + BD} \right).DC}}{2} \)\(= \dfrac{{\left( {1 + 25} \right).6}}{2} = 78\) (đvdt)
Hướng dẫn giải:
+) Vẽ hình trên cùng một hệ trục tọa độ
+) Xác định tọa độ \(C,D\)
+) Tính diện tích hình thang vuông \({\rm{ABCD}}\). Sử dụng công thức tính độ dài \(A\left( {{x_A};{y_A}} \right);B\left( {{x_B};{y_B}} \right) \Rightarrow AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} \)
Câu hỏi khác
- Bài tập hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 toán 9 có lời giải
- Bài tập hệ thức vi-ét và ứng dụng toán 9 có lời giải
- Bài tập phương trình bậc hai một ẩn và công thức nghiệm toán 9 có lời giải
- Bài tập công thức nghiệm thu gọn toán 9 có lời giải
- Bài tập phương trình quy về phương trình bậc hai toán 9 có lời giải
