Trả lời bởi giáo viên
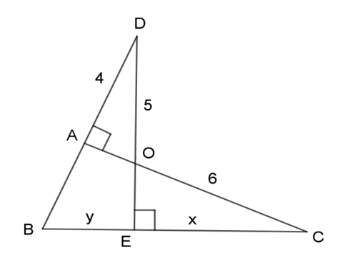
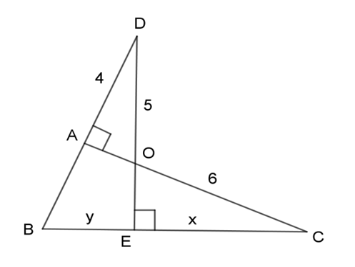
Xét 2 tam giác vuông \(\Delta ADO\)\((\widehat {DAO} = {90^0})\) và \(\Delta ECO\)\((\widehat {CEO} = {90^0})\) ta có:
\(\widehat {AOD} = \widehat {EOC}\) (2 góc đối đỉnh)
\( \Rightarrow \Delta ADO\backsim\Delta ECO\;(g - g)\)
\( \Rightarrow \dfrac{{AD}}{{EC}} = \dfrac{{DO}}{{CO}} \Leftrightarrow \dfrac{4}{x} = \dfrac{5}{6} \Leftrightarrow x = \dfrac{{4.6}}{5} = 4,8\)
Vì \(\Delta ADO\) vuông tại A nên áp dụng định lý Pitago ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,A{D^2} + A{O^2} = O{D^2}\\ \Leftrightarrow {4^2} + A{O^2} = {5^2}\\ \Leftrightarrow A{O^2} = {5^2} - {4^2} = 9\\ \Rightarrow AO = 3\end{array}\)
Xét 2 tam giác vuông \(\Delta CEO\;(\widehat {CEO} = {90^0})\) và \(\Delta CAB\;(\widehat {CAB} = {90^0})\) có:\(\widehat C\) chung
\( \Rightarrow \dfrac{{CO}}{{CB}} = \dfrac{{CE}}{{CA}} \Leftrightarrow \dfrac{{CO}}{{CE + EB}} = \dfrac{{CE}}{{CO + OA}} \Leftrightarrow \dfrac{6}{{4,8 + y}} = \dfrac{{4,8}}{{6 + 3}} \Leftrightarrow y = 6,45\)
Vậy \(x = 4,8;\;y = 6,45\).
Hướng dẫn giải:
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp.
- Tính độ dài $x,y$ dựa vào dữ kiện tìm được và dữ kiện đề bài đã cho (áp dụng định lý Pytago).
Giải thích thêm:
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác.
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.