Câu hỏi:
2 năm trước
Vật kính của một kính hiển có tiêu cự f1 = 1cm, thị kính có tiêu cự f2 = 4cm. Độ dài quang học của kính là 16cm. Mắt đặt sát thị kính. Người quan sát có mắt không bị tật và có khoảng cực cận là Đ = 20cm. Phải đặt vật trong khoảng nào trước vật kính để người quan sát có thể nhìn thấy ảnh của vật qua kính?
Trả lời bởi giáo viên
Đáp án đúng: a
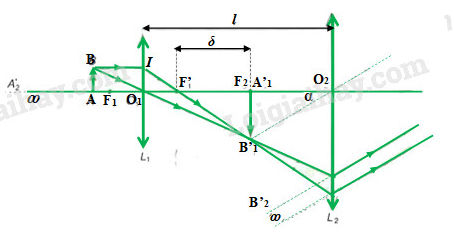
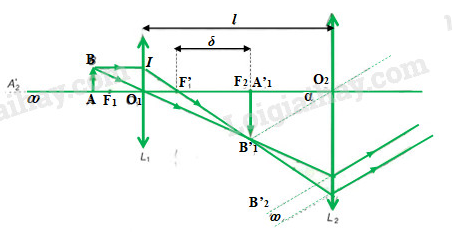
Khoảng cách giữa vật kính và thị kính: \(l = {O_1}{O_2} = \delta + {f_1} + {f_2} = 21cm\)
Các vị trí M, N giới hạn vị trí đặt vật được xác định như sau:
Ta có:
\(\begin{array}{l}{d_{21}}' \to \infty ;{d_{21}} = {f_2} = 4cm;{d_{11}}' = l - {d_{21}} = 17cm\\{d_{11}} = \dfrac{{{d_{11}}'.{f_1}}}{{{d_{11}}' - {f_1}}} = 10,625mm\end{array}\)
Ta có:
\(\begin{array}{l}
{d_{22}}' = - D = - 20cm;;{d_{22}} = \frac{{{d_{22}}'.{f_2}}}{{{d_{22}}' - {f_2}}} = \frac{{10}}{3}cm\\
{d_{12}}' = l - {d_{22}} = \frac{{53}}{3}cm;\frac{1}{{{d_{12}}}} = \frac{1}{{{f_1}}} - \frac{1}{{{d_{12}}'}} = \frac{{50}}{{53}} \Rightarrow {d_{12}} = 1,06cm = 10,6mm
\end{array}\)
Vật chỉ có thể xê dịch trong khoảng: \(\Delta d = {d_{11}} - {d_{12}} = 10,625 - 10,6 = 0,025mm\)
Hướng dẫn giải:
Công thức thấu kính: \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}\)
