Vật có khối lượng \(2kg\) (ban đầu đứng yên) trượt trên sàn có hệ số ma sát \(0,2\) dưới tác dụng của lực không đổi có độ lớn \(10N\) hợp với phương ngang góc \({30^0}\). Lấy \(g = 10m/{s^2}\)

Công của lực ma sát khi vật chuyển động được \(5s\) là:

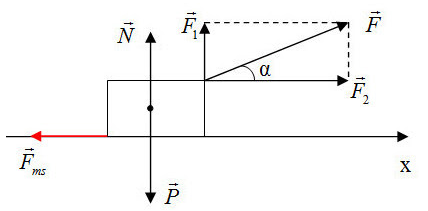
+ Chọn chiều dương là chiều chuyển động của vật

Theo định luật II – Newton ta có: \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{ms}}}  = m\overrightarrow a \)  (1)

+ Chiếu (1) theo các phương, ta được:

- Theo phương Oy: \(N + {F_1} = P \Rightarrow N = P - {F_1}\)

Có \({F_1} = F\sin \alpha \)  ta suy ra \(N = P - F\sin \alpha \)

- Theo phương Ox: \({F_2} - {F_{ms}} = ma\)

Có \({F_2} = F\cos \alpha \), ta suy ra \(Fcos\alpha  - {F_{ms}} = ma\)

Lại có, lực ma sát

\(\begin{array}{l}{F_{ms}} = \mu N = \mu \left( {P - F\sin \alpha } \right)\\ = \mu \left( {mg - F\sin \alpha } \right)\\ = 0,2\left( {2.10 - 10.\sin {{30}^0}} \right)\\ = 3N\end{array}\)

Ta suy ra:

\(\begin{array}{l}Fcos\alpha  - {F_{ms}} = ma\\ \Leftrightarrow Fcos\alpha  - \mu \left( {mg - F\sin \alpha } \right) = ma\\ \Leftrightarrow 10.cos{30^0} - 0,2.\left( {2.10 - 10.\sin {{30}^0}} \right) = 2.a\\ \Rightarrow a = 2,83m/{s^2}\end{array}\)

+ Quãng đường vật di chuyển được từ lúc ban đầu cho đến \(5s\) là: \(s = \dfrac{1}{2}a{t^2} = \dfrac{1}{2}.2,{83.5^2} = 35,375m\)

+ Ta có, góc hợp bởi hướng của lực ma sát và phương chuyển dời của vật là: \({180^0}\)

=> Công của lực ma sát khi vật chuyển động được \(5s\) là: \({A_{{F_{ms}}}} = {F_{ms}}.s.cos{180^0} = 3.35,375.c{\rm{os18}}{{\rm{0}}^0} =  - 106,125N\)