Câu hỏi:
2 năm trước
Vật \(AB = 10cm\) là một đoạn thẳng song song với trục chính của một thấu kính hội tụ mỏng tiêu cự \(f = 20cm\). B gần thấu kính và cách thấu kính \(30cm\). Khoảng cách \(AB\) tới trục chính của thấu kính là \(h = 3cm\). Độ lớn của ảnh là:
Trả lời bởi giáo viên
Đáp án đúng: c
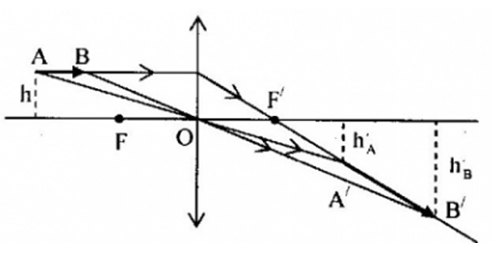
Ta có:
+ Ảnh \(A'B'\) nằm dọc tia ló ứng với tia truyền dọc theo \(AB\)
+ \(\left\{ \begin{array}{l}{d_A} = 30 + 10 = 40cm\\{d_B} = 30cm\end{array} \right.\)
Áp dụng công thức thấu kính: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
Ta suy ra: \(\left\{ \begin{array}{l}{d_A}' = \dfrac{{{d_A}f}}{{{d_A} - f}} = \dfrac{{40.20}}{{40 - 20}} = 40cm\\{d_B}' = \dfrac{{{d_B}f}}{{{d_B} - f}} = \dfrac{{30.20}}{{30 - 20}} = 60cm\end{array} \right.\)
+ Ta suy ra: \(\left\{ \begin{array}{l}\dfrac{{{h_A}}}{h} = \left| { - \dfrac{{{d_A}'}}{{{d_A}}}} \right| = \dfrac{{40}}{{40}} = 1 \to {h_A} = h = 3cm\\\dfrac{{{h_B}}}{h} = \left| { - \dfrac{{{d_B}'}}{{{d_B}}}} \right| = \dfrac{{60}}{{30}} = 2 \to {h_B} = 2h = 6cm\end{array} \right.\)
Ảnh \(A'B'\) là ảnh thật, nghiêng góc với trục chính:
Độ lớn của ảnh:
$\begin{gathered}
A'B' = \sqrt {{{\left( {{d_B}' - {d_A}'} \right)}^2} + {{\left( {{h_B} - {h_A}} \right)}^2}} \hfill \\
= \sqrt {{{\left( {60 - 40} \right)}^2} + {{\left( {6 - 3} \right)}^2}} = 20,2cm \hfill \\
\end{gathered} $
Hướng dẫn giải:
+ Vẽ ảnh của vật qua thấu kính
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính hệ số phóng đại: \(k = - \frac{{d'}}{d}\)
