Câu hỏi:
3 năm trước
Từ một khúc gỗ hình trụ cao$15\,cm$, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là $640\pi \,\,c{m^3}$ .
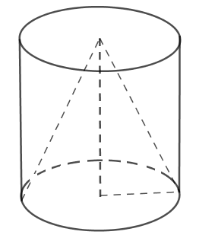
Tính diện tích xung quanh của hình nón.
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có \({V_t} = \pi {R^2}h = 960\pi \)
\(\Leftrightarrow \pi {R^2}.15 = 960\pi \)
\( \Rightarrow R = 8\,cm\) nên bán kính đáy của hình nón là \(R = 8\,cm\).
Chiều cao hình nón \(h = 15\,cm\) \( \Rightarrow \) đường sinh hình nón \({l^2} = {h^2} + {R^2} \Rightarrow l = 17\,cm\)
Diện tích xung quanh hình nón là \(S = \pi Rl = \pi .8.17 = 136\pi \,\left( {c{m^2}} \right)\) .
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\) để tìm bán kính đáy
Sử dụng công thức tính diện tích xung quanh hình nón \(S = \pi Rl\).

