Câu hỏi:
2 năm trước
Trong mặt phẳng với hệ toạ độ $Oxy,$ cho tam giác $ABC$ có phương trình đường phân giác trong góc $A$ là ${d_1}:x + y + 2 = 0,$ phương trình đường cao vẽ từ $B$ là ${d_2}:2x-y + 1 = 0,$ cạnh $AB$ đi qua $M\left( {1;-1} \right).$ Tìm phương trình cạnh $AC.$
Trả lời bởi giáo viên
Đáp án đúng: c
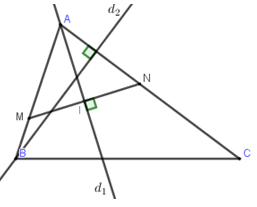
Gọi $N$ là điểm đối xứng của $M$ qua \({d_1} \Rightarrow N \in AC\)
\(\overrightarrow {MN} = ({x_N} - 1,\,\,{y_N} + 1)\)
Ta có: \(\overrightarrow {MN} \) cùng phương \({\overrightarrow n _{{d_1}}} = (1;\,\,1)\)
\( \Leftrightarrow \,\,1({x_N} - 1) - 1({y_N} + 1) = 0\)\( \Leftrightarrow {x_N} - {y_N} = 2\,\,\,(1)\)
Tọa độ trung điểm $I$ của \(MN:\)\({x_I} = \dfrac{1}{2}\left( {1 + {x_N}} \right),{y_I} = \dfrac{1}{2}\left( { - 1 + {y_N}} \right)\)
\(I \in \left( {{d_1}} \right) \Leftrightarrow \dfrac{1}{2}\left( {1 + {x_N}} \right) + \dfrac{1}{2}\left( { - 1 + {y_N}} \right) + 2 = 0\)\( \Leftrightarrow {x_N} + {y_N} + 4 = 0\,\,\,\,(2)\)
Giải hệ $\left( 1 \right)$ và $\left( 2 \right)$ ta được $N\left( {-1;-3} \right)$
Phương trình cạnh $AC$ vuông góc với \({d_2}\) có dạng: $x + 2y + C = 0.$
\(N \in AC\)\( \Leftrightarrow - 1 + 2.( - 3) + C = 0\)\( \Leftrightarrow C = 7\)
Vậy, phương trình cạnh $AC:$ $x + 2y + 7 = 0.$
Hướng dẫn giải:
- Gọi \(N\) là điểm đối xứng của \(M\) qua đường phân giác trong \({d_1}\)
- Từ hai điều kiện \(\overrightarrow {MN} \) cùng phương \(\overrightarrow {{n_{{d_1}}}} \) và trung điểm của \(MN\) là \(I \in {d_1}\) ta tìm \(N\)
- Viết phương trình \(AC\) vuông góc \({d_2}\) và đi qua \(N\)
