Câu hỏi:
2 năm trước
Trong mặt phẳng \(Oxy\), cho hai đường tròn : \(\left( {{C_1}} \right):\quad {x^2} + {y^2} = 13\) và \(\left( {{C_2}} \right):\;{\left( {x - 6} \right)^2} + {y^2} = 25\) cắt nhau tại \(A\left( {2;3} \right)\).Viết phương trình tất cả đường thẳng\(d\) đi qua \(A\) và cắt \(\left( {{C_1}} \right),\;\left( {{C_2}} \right)\) theo hai dây cung có độ dài bằng nhau.
Trả lời bởi giáo viên
Đáp án đúng: a
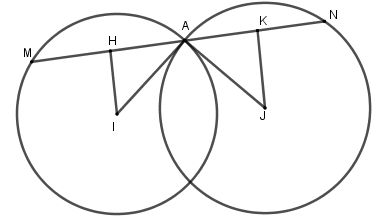
- Từ giả thiết : \(\left( {{C_1}} \right):\;I = \left( {0;0} \right),R = \sqrt {13} .\left( {{C_2}} \right);J\left( {6;0} \right),R' = 5\)
- Gọi đường thẳng \(d\) qua \(A\left( {2;3} \right)\) có véc tơ chỉ phương \(\overrightarrow n = \left( {a;b} \right)\) \( \Rightarrow d:a\left( {x - 2} \right) + b\left( {y - 3} \right) = 0\) \( \Leftrightarrow ax + by - 2a - 3b = 0\).
Dễ thấy \(AH = AK\) (vì \(AM = AN\)) nên $I{A^2} - I{H^2} = J{A^2} - J{K^2}$ \( \Leftrightarrow 13 - {d^2}\left( {I,d} \right) = 25 - {d^2}\left( {J,d} \right)\) \( \Leftrightarrow {d^2}\left( {J,d} \right) - {d^2}\left( {I,d} \right) = 12\).
Mà \(d\left( {I,d} \right) = \dfrac{{\left| { - 2a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) và \(d\left( {J,d} \right) = \dfrac{{\left| {4a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) nên:
\(\dfrac{{16{a^2} - 24ab + 9{b^2}}}{{{a^2} + {b^2}}} - \dfrac{{4{a^2} + 12ab + 9{b^2}}}{{{a^2} + {b^2}}} = 12\) \( \Leftrightarrow 12{a^2} - 36ab = 12{a^2} + 12{b^2}\)
\( \Leftrightarrow 12{b^2} = - 36ab \Leftrightarrow \left[ \begin{array}{l}b = 0\\b = - 3a\end{array} \right.\).
Nếu \(b = 0\) thì chọn \(a = 1\) ta được phương trình \(x - 2 = 0\).
Nếu \(b = - 3a\) thì chọn \(a = 1\) ta được \(b = - 3\), ta được phương trình \(x - 3y + 7 = 0\).
Vậy có 2 đường thẳng: \({d_1}:x - 2 = 0\) và \({d_2}:x - 3y + 7 = 0\).
Hướng dẫn giải:
- Viết dạng phương trình của đường thẳng \(d\) đi qua \(A\) và có VTPT \(\overrightarrow n = \left( {a;b} \right)\).
- Sử dụng mối quan hệ hai dây cung có độ dài bằng nhau suy ra mối quan hệ giữa hai khoảng cách từ hai tâm đến đường thẳng.
- Lập phương trình ẩn \(a,b\) và chọn bộ \(a,b\) thích hợp rồi kết luận.
Câu hỏi khác
- Đề thi kiểm tra 1 tiết chương 9: Phương pháp tọa độ trong mặt phẳng - Đề số 1 Toán 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 9: Phương pháp tọa độ trong mặt phẳng - đề số 3 Toán 10 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 9: Phương pháp tọa độ trong mặt phẳng - Đề số 1 Toán 10 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 9: Phương pháp tọa độ trong mặt phẳng - đề số 3 Toán 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 9: Phương pháp tọa độ trong mặt phẳng - đề số 2 Toán 10 có lời giải chi tiết
