Câu hỏi:
2 năm trước
Trong không gian \(Oxyz\), tập hợp các điểm \(M\left( {a;b;c} \right)\) sao cho \({a^2} + {b^2} \le 2,\,\,\left| c \right| \le 8\) là một khối tròn xoay. Tính thể tích của khối tròn xoay đó?
Trả lời bởi giáo viên
Đáp án đúng: c
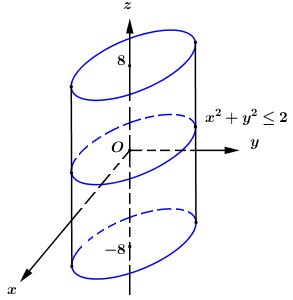
Tập hợp các điểm \(M\left( {a;b;c} \right)\) sao cho \({a^2} + {b^2} \le 2,\,\,\left| c \right| \le 8\) là khối trụ có bán kính đáy \(r = \sqrt 2 \), chiều cao \(h = 16\).
Do đó thể tích khối trụ là \(V = \pi {r^2}h = \pi .{\left( {\sqrt 2 } \right)^2}.16 = 32\pi \).
Hướng dẫn giải:
Thể tích khối trụ có chiều cao \(h\), bán kính đáy \(r\) là \(V = \pi {r^2}h\).
Câu hỏi khác
- Đề thi kiểm tra 1 tiết chương 6: Mặt nón, mặt trụ, mặt cầu - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 3 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 6: Mặt nón, mặt trụ, mặt cầu - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 2 Toán 12 có lời giải chi tiết
