Câu hỏi:
2 năm trước
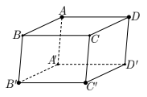
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(0;0;1), B’(1;0;0), C’(1;1;0). Tìm tọa độ điểm D.
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có AD // B’C’, AD = B’C’ nên AB’C’D là hình bình hành, do đó AB’ // DC’ và AB’ = DC’.
⇒→AB′=→DC′⇒{1−0=1−xD0−0=1−yD0−1=0−zD⇒{xD=0yD=1zD=1
Vậy D(0;1;1).
Hướng dẫn giải:
- Sử dụng định nghĩa hai vectơ bằng nhau là hai vectơ cùng hướng và có độ lớn bằng nhau.
- Hai vectơ bằng nhau khi và chỉ khi hoành độ, tung độ, cao độ tương ứng của chúng bằng nhau.

