Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = {\log _{2020}}\left( {mx - m + 2} \right)\) xác định trên \(\left[ {1; + \infty } \right).\)

ĐKXĐ: \(mx - m + 2 > 0 \Leftrightarrow m\left( {x - 1} \right) >  - 2\)

Để hàm số xác định trên \(\left[ {1; + \infty } \right)\) thì \(m\left( {x - 1} \right) >  - 2\,\,(*),\,\,\forall x \ge 1\)

+) \(x = 1 \Rightarrow \) (*) \( \Leftrightarrow 0m >  - 2\) đúng với mọi m

+) \(x > 1 \Rightarrow \) (*) \( \Leftrightarrow m > \dfrac{{ - 2}}{{x - 1}}\), \(\forall x > 1\) (2*).

Xét hàm số \(f\left( x \right) = \dfrac{{ - 2}}{{x - 1}}\,\,\forall x > 1\)ta có \(f'\left( x \right) = \dfrac{2}{{{{\left( {x - 1} \right)}^2}}} > 0\,\,\forall x \in \left( {1; + \infty } \right)\).

BBT:

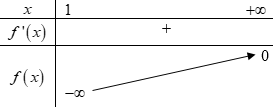
Dựa vào BBT \( \Rightarrow m \ge 0\).

Vậy để hàm số \(y = {\log _{2020}}\left( {mx - m + 2} \right)\) xác định trên \(\left[ {1; + \infty } \right)\) thì \(m \ge 0\).