Câu hỏi:
2 năm trước
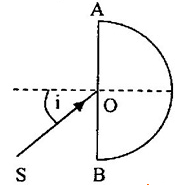
Tiết diện thẳng của một khối đồng chất, trong suốt nưa hình trụ là nửa hình tròn tâm O, bán kính R, khối này làm bằng chất có chiết suất \(n = \sqrt 2 \), đặt trong không khí. Tia sáng \(SI\) nằm trong mặt phẳng vuông góc với trục của hình trụ, tới mặt phẳng của khối này với góc tới \(i = {45^0}\). Góc lệch D giữa tia tới và tia ló ra khỏi bán trụ có giá trị là bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: d
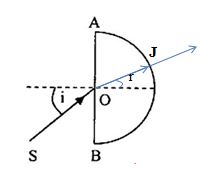
Với điểm tới O – tâm của bán trụ
=> Tia khúc xạ OJ chính là bán kính của đường tròn nên thẳng góc với mặt cầu tại J => OJ truyền thẳng qua bán trụ
+ Theo định luật khúc xạ ánh sáng, ta có:
\(\begin{array}{l}{n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Leftrightarrow 1.\sin {45^0} = \sqrt 2 {\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = \dfrac{1}{2} \Rightarrow r = {30^0}\end{array}\)
=> Góc lệch giữa tia tới và tia ló ra khỏi bán cầu là: \(D = i - r = {45^0} - {30^0} = {15^0}\)
Hướng dẫn giải:
Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
