Câu hỏi:
2 năm trước
Tam giác \(ABC\) có đoạn thẳng nối trung điểm của \(AB\) và \(BC\) bằng \(3\), cạnh \(AB = 9\) và \(\widehat {ACB} = 60^\circ \). Tính độ dài cạnh cạnh \(BC\).
Trả lời bởi giáo viên
Đáp án đúng: a
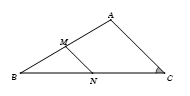
Bước 1: Tính \(AC\)
Gọi \(M,\;N\) lần lượt là trung điểm của \(AB,\;BC\).
\( \Rightarrow MN\) là đường trung bình của \(\Delta ABC\).
\( \Rightarrow MN = \dfrac{1}{2}AC\). Mà \(MN = 3\), suy ra \(AC = 6\).
Bước 2: Sử dụng định lý cô sin cho tam giác \(ABC\)
Theo định lí hàm cosin, ta có
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}\\ \Leftrightarrow {9^2} = {6^2} + B{C^2} - 2.6.BC.\cos 60^\circ \\ \Rightarrow BC = 3 + 3\sqrt 6 \end{array}\)
Hướng dẫn giải:
Bước 1: Tính \(AC\)
Bước 2: Sử dụng định lý cô sin cho tam giác \(ABC\)

