Tại hai điểm \(A\) và \(B\) ở mặt chất lỏng có \(2\) nguồn kết hợp dao động điều hòa theo phương thẳng đứng và cùng pha. \(Ax\) là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với \(AB\). Trên \(Ax\) có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó \(M\) là điểm xa \(A\) nhất, \(N\) là điểm kế tiếp với \(M\), \(P\) là điểm kế tiếp với \(N\) và \(Q\) là điểm gần \(A\) nhất. Biết  \(MN{\rm{ }} = {\rm{ }}22,25{\rm{ }}cm\) và \(NP{\rm{ }} = {\rm{ }}8,75{\rm{ }}cm\). Độ dài đoạn \(QA\) gần nhất với giá trị nào sau đây?

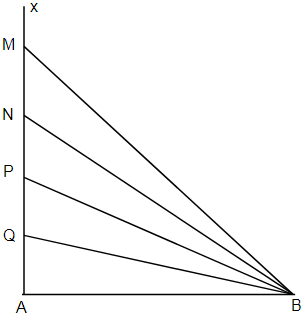
+ Ta thấy trên nửa đường thẳng kẻ từ \(A\) vuông góc với \(AB\) có \(4\) điểm theo thứ tự \(M,N,P,Q\) dao động với biên độ cực đại

=> Nên \(AB\) có \(9\) điểm dao động với biên độ cực đại với: \( - 4 \le k \le 4\left( {{d_2} - {d_1} = k\lambda } \right)\)

Cực đại $M,N,P,Q$ ứng với $k = 1,2,3,4$

+ Đặt $AB = a$

Tại $C$ trên \(Ax\) là điểm dao động với biên độ cực đại:

\(CB - CA = k\lambda \left( * \right)\)

\(\begin{array}{l}C{B^2} - C{A^2} = {a^2}\\ \to \left( {CB - CA} \right)\left( {CB + CA} \right) = {a^2}\\ \to CB + CA = \dfrac{{{a^2}}}{{k\lambda }}\left( {**} \right)\end{array}\)

Từ \(\left( * \right)\) và \(\left( {**} \right)\) ta suy ra: \(CA = \dfrac{{{a^2}}}{{2k\lambda }} - \dfrac{{k\lambda }}{2}\)

- Tại \(M\) ứng với \(k = 1\): \(MA = \dfrac{{{a^2}}}{{2\lambda }} - \dfrac{\lambda }{2}\left( 1 \right)\)

- Tại \(N\) ứng với \(k = 2\): \(NA = \dfrac{{{a^2}}}{{2.2\lambda }} - \dfrac{{2\lambda }}{2} = \dfrac{{{a^2}}}{{4\lambda }} - \lambda \left( 2 \right)\)

- Tại \(P\) ứng với \(k = 3\): \(PA = \dfrac{{{a^2}}}{{2.3\lambda }} - \dfrac{{3\lambda }}{2} = \dfrac{{{a^2}}}{{6\lambda }} - \dfrac{{3\lambda }}{2}\left( 3 \right)\)

- Tại \(Q\) ứng với \(k = 4\): \(QA = \dfrac{{{a^2}}}{{2.4\lambda }} - \dfrac{{4\lambda }}{2} = \dfrac{{{a^2}}}{{8\lambda }} - 2\lambda \left( 4 \right)\)

Lấy \(\left( 1 \right) - \left( 2 \right)\) ta được: \(MN = MA - NA = \dfrac{{{a^2}}}{{4\lambda }} + \dfrac{\lambda }{2} = 22,25cm\left( 5 \right)\)

Lấy \(\left( 2 \right) - \left( 3 \right)\) ta được: \(NP = NA - PA = \dfrac{{{a^2}}}{{12\lambda }} + \dfrac{\lambda }{2} = 8,75cm\left( 6 \right)\)

Lấy \(3.\left( 6 \right) - \left( 5 \right)\) ta được:

\(\begin{array}{l}3\left( {\dfrac{{{a^2}}}{{12\lambda }} + \dfrac{\lambda }{2}} \right) - \left( {\dfrac{{{a^2}}}{4} + \dfrac{\lambda }{2}} \right) = 3.8,75 - 22,25\\ \to \lambda  = 4cm\end{array}\)

Lấy \(\left( 5 \right) - \left( 6 \right)\) ta được: \(\dfrac{{{a^2}}}{{6\lambda }} = 22,25 - 8,75 = 13,5cm \to \dfrac{{{a^2}}}{\lambda } = 81cm\)

Thay \(\left\{ \begin{array}{l}\lambda  = 4cm\\\dfrac{{{a^2}}}{\lambda } = 81cm\end{array} \right.\) vào \(\left( 4 \right)\) ta được: \(QA = \dfrac{{{a^2}}}{{8\lambda }} - 2\lambda  = \dfrac{{81}}{8} - 2.4 = 2,125cm\)