Sóng truyền theo phương ngang trên một sợi dây dài với tần số $10Hz$. Điểm $M$ trên dây tại một thời điểm đang ở vị trí cao nhất và tại thời điểm đó điểm $N$ cách $M$ $5cm$ đang đi qua vị trí có li độ bằng nửa biên độ và đi lên. Coi biên độ sóng không đổi khi truyền. Biết khoảng cách $MN$ nhỏ hơn bước sóng của sóng trên dây. Chọn đáp án đúng cho tốc độ truyền sóng và chiều truyền sóng.
Trả lời bởi giáo viên
Ta có:
+ Điểm $M$ ở vị trí cao nhất tức là biên dương.
+ Điểm $N$ qua vị trí có li độ bằng $\dfrac{A}{2}$ và đang đi lên
Vẽ trên vòng tròn lượng giác, ta được:
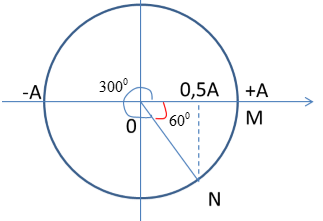
Ta có 2 trường hợp của góc lệch pha giữa $M$ và $N$:
+ TH 1: $M, N$ lệch pha nhau: $60^0$:
\(\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{\pi }{3} \to \lambda = 6\Delta d = 6.5 = 30cm\\ \to v = \lambda f = 30.10 = 300cm/s = 3m/s\end{array}\)
$M$ sớm pha hơn $N$ => Sóng truyền từ $M$ đến $N$
+ TH 2: $M, N$ lệch pha nhau $300^0$:
\(\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{5\pi }}{3} \to \lambda = \dfrac{6}{5}\Delta d = \dfrac{6}{5}.5 = 6cm\\ \to v = \lambda f = 6.10 = 60cm/s\end{array}\)
Do $N$ sớm pha hơn $M$
=> Sóng truyền từ $N$ đến $M$
Hướng dẫn giải:
+ Sử dụng vòng tròn lượng giác.
+ Vận dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }\)
+ Áp dụng công thức tính tốc độ truyền sóng: \(v = \lambda f\)

