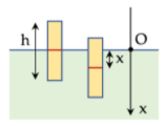
Một vật hình trụ tiết diện nhỏ, có chiều cao \(20\;{\rm{cm}}\), nổi thẳng đứng trong một bể nước rộng. Bỏ qua mọi lực cản, lấy \(g = 10\;{\rm{m}}/{{\rm{s}}^2}\). Khi cân bằng, một nửa vật bị chìm trong nước và mép dưới của vật cách đáy bể một đoạn đủ dài. Từ vị trí cân bằng của vật, truyền cho nó vận tốc ban đầu bằng \(1,5\;{\rm{m}}/{\rm{s}}\) hướng thẳng đứng xuống dưới. Kể từ lúc vật bắt đầu chuyển động đến lúc vận tốc của vật triệt tiêu lần đầu tiên thì tốc độ trung bình của vật gần nhất với giá trị nào sau đây?

Một con lắc đơn gồm một vật nhỏ khối lượng \(m = 2g\) và một dây treo mảnh, chiều  dài \(l\) , được kích thích cho dao động điều hòa, Trong khoảng thời gian Δt con lắc thực hiện được \(40\) dao động. Khi tăng chiều dài con lắc thêm một đoạn \(7,9cm\)  thì cũng trong khoảng thời gian Δt con lắc thực hiện được \(39\) dao động. Lấy gia tốc trọng trường \(g{\rm{ }} = {\rm{ }}9,8m/{s^2}\). Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc chiều dài \(l\), người ta truyền cho vật điện tích \(q{\rm{ }} = {\rm{ }} + {\rm{ }}{0,5.10^{ - 8}}C\) rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Vecto cường độ điện trường này có

Một con lắc đơn có chiều dài \(1{\rm{ }}m\), đầu trên cố định đầu dưới gắn với vật nặng có khối lượng m. Điểm cố định cách mặt đất \(2,5{\rm{ }}m\). Ở thời điểm ban đầu đưa con lắc lệch khỏi vị trí cân bằng một góc \(a = {\rm{ }}0,09{\rm{ }}rad\), rồi thả nhẹ khi con lắc vừa qua vị trí cân bằng thì sợi dây bị đứt. Bỏ qua mọi sức cản, lấy \(g{\rm{ }} = {\rm{ }}9,8{\rm{ }}m/{s^2}\). Tốc độ của vật nặng ở thời điểm \(t{\rm{ }} = {\rm{ }}0,08{\rm{ }}s\) có giá trị gần bằng:

Một con lắc gồm lò xo nhẹ có độ cứng \(k{\rm{ }} = {\rm{ }}50{\rm{ }}N/m\) một đầu cố định, đầu kia gắn với một  vật nhỏ khối lượng \({m_1} = {\rm{ }}m\) đặt trên mặt phẳng nằm ngang không ma sát. Ban đầu kéo lò xo dãn một đoạn \(10cm\)  rồi buông nhẹ để $m$ dao động điều hòa. Ở thời điểm lò xo có chiều dài cực tiểu, ta đặt nhẹ vật \({m_2} = {\rm{ }}3m\) lên trên \({m_1}\), sau đó cả hai cùng dao động điều hòa với vận tốc cực đại \(50\sqrt 2 cm/s\) . Giá trị của $m$ là:

Một lò xo độ cứng \(k = 50{\rm{ }}N/m\), một đầu cố định, đầu còn lại treo vật nặng khối lượng \(m = 100g\). Điểm treo lò xo chịu được lực tối đa không quá \(4N\). Lấy \(g = 10m/{s^2}\). Để hệ thống không bị rơi thì vật nặng dao động theo phương thẳng đứng với biên độ không quá:

Một con lắc đơn gồm một vật nhỏ có khối lượng \(m = 2{\rm{ }}g\) và một dây treo mảnh, chiều dài \(l\), được kích thích cho dao động điều hòa. Trong khoảng thời gian \(\Delta t\) con lắc thực hiện được \(40\) dao động. Khi tăng chiều dài con lắc thêm một đoạn bằng \(7,9cm\), thì cũng trong khoảng thời gian $Δt$ con lắc thực hiện được 39 dao động. Lấy gia tốc trọng trường \(g = 9,8{\rm{ }}m/{s^2}\). Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc có chiều dài \(l\), người ta truyền cho vật điện tích \(q =  - {10^{ - 8}}C\) rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Véc tơ cường độ điện trường này có

Trong thang máy, tại trần người ta treo một con lắc lò xo có độ cứng \(k{\rm{ }} = {\rm{ }}25{\rm{ }}N/m\), vật nặng có khối lượng \(400{\rm{ }}g\). Khi thang máy đứng yên ta cho con lắc dao động điều hòa, chiều dài con lắc thay đổi từ \(32{\rm{ }}cm\) đến \(48{\rm{ }}cm\). Tại thời điểm mà vật ở vị trí thấp nhất thì cho thang máy đi xuống nhanh dần đều với gia tốc \(a = \dfrac{g}{{10}}\) . Lấy \(g = {\pi ^2}m/{s^2} = 10{\rm{ }}m/{s^2}\). Biên độ dao động của vật trong trường hợp này là:

Một con lắc đơn gồm sợi dây mảnh dài \(l = 1m\), vật có khối lượng \(m = 100\sqrt 3 g\) tích điện \(q = {10^{ - 5}}\left( C \right)\). Treo con lắc đơn trong điện trường đều có phương vuông góc với gia tốc trọng trường \(\overrightarrow g \) và có độ lớn \(E = {10^5}V/m\). Kéo vật theo chiều của vec tơ điện trường sao cho góc tạo bởi dây treo của con lắc và \(\overrightarrow g \) bằng \({60^0}\) rồi thả nhẹ để vật dao động. Lực căng cực đại của dây treo là: