Câu hỏi:
2 năm trước
Một vật có khối lượng \(m = 200g\) gắn vào lò xo dao động điều hòa có đồ thị li độ theo thời gian như hình vẽ:
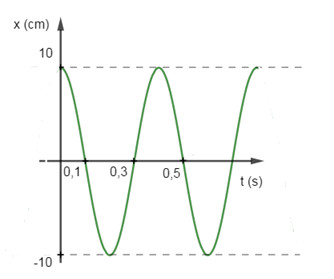
Động năng của vật tại thời điểm \(t = 0,5s\) là:
Trả lời bởi giáo viên
Đáp án đúng: b
+ Từ đồ thị, ta có:
- Biên độ dao động của vật: \(A = 10cm\)
- Khoảng thời gian từ \(0,1s\) đến \(0,3s\): \(\Delta t = 0,3 - 0,1 = 0,2s = \dfrac{T}{2} \to T = 0,4s\)
- Tần số góc của dao động: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,4}} = 5\pi \left( {rad/s} \right)\)
+ Tại thời điểm \(t = 0,5s\) vật đang ở li độ \(x = 0\)
=> Thế năng của vật khi đó: \({{\rm{W}}_t} = \dfrac{1}{2}k{x^2} = 0J\)
=> Động năng của vật khi đó:
\(\begin{array}{l}{{\rm{W}}_d} = {\rm{W}} = \dfrac{1}{2}k{A^2} = \dfrac{1}{2}m{\omega ^2}{A^2}\\ = \dfrac{1}{2}.0,2.{\left( {5\pi } \right)^2}.{\left( {0,1} \right)^2} = 0,25J\end{array}\)
Hướng dẫn giải:
+ Đọc đồ thị dao động, xác định các đại lượng: Biên độ, chu kì
+ Sử dụng biểu thức tính tần số góc: \(\omega = \dfrac{{2\pi }}{T}\)
+ Xác định li độ của vật tại thời điểm \(t = 0,5s\)
+ Sử dụng biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2} = {\rm{W}} - {{\rm{W}}_t}\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
