Một vật có khối lượng \(m = 100g\) trượt không vận tốc đầu từ đỉnh xuống chân một mặt phẳng nghiêng dài \(l = 2m\), chiều cao \(h = 0,4m\). Vận tốc ở chân mặt phẳng nghiêng là \(2m/s\). Công của lực ma sát có giá trị là:

Chọn chiều dương là chiều chuyển động của vật, gắn hệ trục tọa độ như hình vẽ

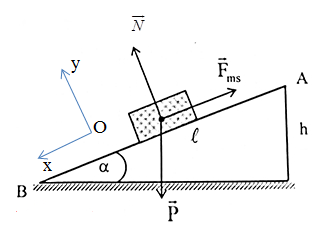
Ta có:

+ Góc nghiêng của mặt phẳng nghiêng \(\alpha \), với \(\sin \alpha  = \dfrac{h}{l} = \dfrac{{0,4}}{2} = 0,2\)

+ Vận tốc của vật ở đỉnh mặt phẳng nghiêng \({v_0} = 0m/s\)

Vận tốc của vật ở chân dốc \(v = 2m/s\)

Áp dụng hệ thức liên hệ, ta có: \({v^2} - v_0^2 = 2al\)

Ta suy ra: \(a = \dfrac{{{v^2} - v_0^2}}{{2l}} = \dfrac{{{2^2} - 0}}{{2.2}} = 1m/{s^2}\)

+ Theo định luật II – Newton ta có: \(\overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{ms}}}  = m\overrightarrow a \)  (1)

Chiếu (1) theo các phương, ta được:

- Theo phương Oy: \(N - {P_y} = 0 \Rightarrow N = {P_y} = P\cos \alpha \)

- Theo phương Ox:

\(\begin{array}{l}{P_x} - {F_{ms}} = ma\\ \Rightarrow {F_{ms}} = {P_x} - ma = P\sin \alpha  - ma\\ = mg\sin \alpha  - ma\\ = 0,1.10.0,2 - 0,1.1 = 0,1N\end{array}\)

+ Góc hợp bởi \(\overrightarrow {{F_{ms}}} \) và chiều dịch chuyển của vật là \({180^0}\) 

=> Công của lực ma sát: \({A_{{F_{ms}}}} = {F_{ms}}.lcos{180^0} = 0,1.2.cos{180^0} =  - 0,2J\)