Câu hỏi:
2 năm trước
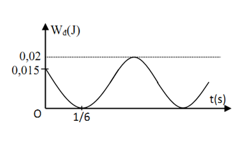
Một vật có khối lượng $400g$ dao động điều hòa có đồ thị động năng như hình vẽ. Tại thời điểm $t = 0$ vật đang chuyển động theo chiều dương, lấy $\pi^2=10$. Phương trình dao động của vật là:
Trả lời bởi giáo viên
Đáp án đúng: d
Từ đồ thị, ta có:
+ Tại thời điểm ban đầu (t =0) :
\(\begin{array}{l}{{\rm{W}}_d} = 0,015 \to {{\rm{W}}_t} = 0,02 - 0,015 = {5.10^{ - 3}}J = \dfrac{{\rm{W}}}{4}\\ \to {x_0} = \pm \dfrac{A}{2}\end{array}\)
+ Vị trí có Wđ = 0 lần thứ nhất: <=> x1 = ±A
Dựa vào đồ thị ta suy ra: x0 = A/2 và x1 = A
=> Khoảng thời gian vật đi từ x0 đến x1 là:
\(\Delta t = \dfrac{T}{6} = \dfrac{1}{6}s \to T = 1{\rm{s}} \to \omega = \dfrac{{2\pi }}{T} = 2\pi (ra{\rm{d}}/s)\)
\({{\rm{W}}_{{{\rm{d}}_{{\rm{max}}}}}} = \dfrac{1}{2}m{\omega ^2}{A^2} = 0,02 \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{d_{{\rm{max}}}}}}}}{{m{\omega ^2}}}} = \sqrt {\dfrac{{2.0,02}}{{0,4.{{(2\pi )}^2}}}} = 0,05m = 5cm\)
Tại t = 0:
\(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi {\rm{ = }}\dfrac{A}{2}\\v = - {\rm{Asin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{3}\)
=> Phương trình dao động của vật: \(x = 5c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{3}} \right)cm\)
Hướng dẫn giải:
+ Đọc đồ thị Wđ - t
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\)
+ Áp dụng biểu thức tính động năng cực đại: \({{\rm{W}}_{{{\rm{d}}_{{\rm{max}}}}}} = \dfrac{1}{2}m{\omega ^2}{A^2}\)
+ Viết phương trình dao động điều hòa
Câu hỏi khác
- Bài tập đại cương về dao động điều hòa tự chọn ĐGTD ĐHBK HN có lời giải
- Bài tập năng lượng, vận tốc, lực của con lắc đơn tự chọn ĐGTD ĐHBK HN có lời giải
- Bài tập con lắc đơn tự chọn ĐGTD ĐHBK HN có lời giải
- Bài tập viết phương trình dao động điều hòa tự chọn ĐGTD ĐHBK HN có lời giải
- Bài tập con lắc lò xo tự chọn ĐGTD ĐHBK HN có lời giải
