Câu hỏi:
2 năm trước
Một người nhìn hòn sỏi dưới đáy một bể nước thấy ảnh của nó dường như cách mặt nước một khoảng \(1,2m\), chiết suất của nước là \(n = \dfrac{4}{3}\). Độ sâu của bể là:
Trả lời bởi giáo viên
Đáp án đúng: c
Gọi S là hòn sỏi dưới đấy bể, S’ là ảnh của S. Để có ảnh rõ góc tới i phải nhỏ
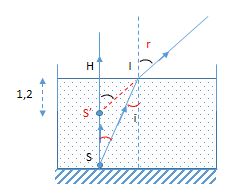
Ta có: \(\dfrac{{Sini}}{{Sinr}} = \dfrac{{{n_2}}}{{{n_1}}}\)(1)
Mặt khác: \(\tan i = \dfrac{{HI}}{{HS}};{\mathop{\rm tanr}\nolimits} = \dfrac{{HI}}{{HS'}} = > \dfrac{{\tan i}}{{\tan {\rm{r}}}} = \dfrac{{HS'}}{{HS}}\)(2)
Vì góc tới i nhỏ nên: $\tan i \sim \sin i;\operatorname{t} {\text{anr}} \sim \operatorname{s} {\text{inr}}$
Từ (1) và (2): \(\dfrac{{{n_2}}}{{{n_1}}} = \dfrac{{HS'}}{{HS}} = > HS = \dfrac{{{n_1}}}{{{n_2}}}.HS' = \dfrac{4}{3}.1,2 = 1,6m = 16dm\)
Hướng dẫn giải:
- Vẽ hình, sử dụng định luật khúc xạ ánh sáng và hệ thức lượng giác trong tam giác vuông
- Tính HS
