Câu hỏi:
2 năm trước
Một người ngồi trên bờ hồ nhúng chân vào nước trong suốt. Biết chiết suất của nước là \(\dfrac{4}{3}\). Người này cao \(1,68m\), nhìn thấy một hòn sỏi dưới đáy hồ dường như cách mặt nước \(1,5m\). Hỏi nếu đứng dưới hồ thì người ấy có bị ngập đầu không? Chiều cao của nước trong hồ là bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có: \(\left\{ \begin{array}{l}{n_1} = \dfrac{4}{3}\\{n_2} = 1\end{array} \right.;HA' = 1,5m\)
Tia sáng đi từ hòn sỏi đi vào mắt người
Gọi:
+ A : là vị trí của hòn sỏi
+ A’: ảnh của hòn sỏi
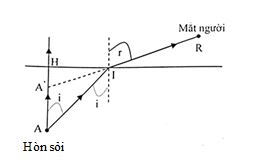
=> Để nhìn rõ thì góc r, i rất nhỏ
\( \to \tan i \approx \sin i \approx i;{\rm{ }}{\mathop{\rm t}\nolimits} {\rm{anr}} \approx {\mathop{\rm s}\nolimits} {\rm{inr}} \approx r\)
Từ hình, ta có: \(\left\{ \begin{array}{l}\tan i = \dfrac{{HI}}{{HA}}\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \dfrac{{HI}}{{HA'}}\end{array} \right.\)
Theo định luật khúc xạ ánh sáng, ta có:
\(\begin{array}{l}\dfrac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \dfrac{{{n_2}}}{{{n_1}}} \approx \dfrac{{\tan i}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} \leftrightarrow \dfrac{1}{{\dfrac{4}{3}}} = \dfrac{{\dfrac{{HI}}{{HA}}}}{{\dfrac{{HI}}{{HA'}}}} = \dfrac{{HA'}}{{HA}}\\ \to HA = \dfrac{4}{3}HA' = \dfrac{4}{3}.1,5 = 2m\end{array}\)
=> Nước trong hồ cao 2m
Theo đầu bài, người cao 1,68m < 2m
=> Nếu người đứng dưới hồ thì người đó sẽ bị ngập đầu
Hướng dẫn giải:
+ Sử dụng các hệ thức lượng trong tam giác:
+ Vận dụng biểu thức của định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
