Câu hỏi:
2 năm trước
Một ngọn đèn nhỏ \(S\) đặt ở đáy một bể nước \(\left( {n = \dfrac{4}{3}} \right)\), độ cao mực nước \(h{\rm{ }} = {\rm{ }}60{\rm{ }}cm\). Bán kính \(r\) bé nhất của tấm gỗ tròn nổi trên mặt nước sao cho không một tia sáng nào từ \(S\) lọt ra ngoài không khí là:
Trả lời bởi giáo viên
Đáp án đúng: b
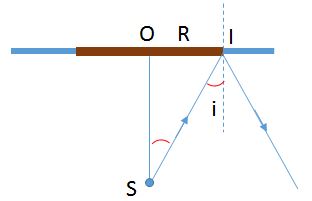
- Không có một tia sáng nào từ S lọt ra ngoài không khí khi tia sáng từ S tới mặt nước bị phản xạ toàn phần
=> \(i \ge {i_{gh}}\) với \(sin{i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{1}{{4/3}} = \dfrac{3}{4} \to {i_{gh}} = {48^0}35'\)
- Xét tam giác vuông SOI: \(tani = \dfrac{{OI}}{{OS}} = \dfrac{R}{{60}} \to R = 60.\tan i\)
- Rmin \( \leftrightarrow \) tani min \( \leftrightarrow \) imin = igh =>
\({R_{\min }} = 60.\tan {i_{\min }} = 60.\tan {i_{gh}} = 60.\tan {48^o}35' \sim 68cm\)
Hướng dẫn giải:
Sử dụng lí thuyết về điều kiện xảy ra hiện tượng phản xạ toàn phần:
+ \({n_1} > {n_2}\)
+ \(i \ge {i_{gh}}\) với \(sin{i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}\)
