Câu hỏi:
2 năm trước
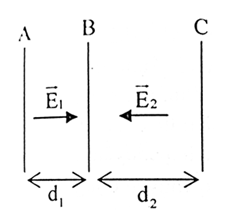
Một êlectron di chuyển trong điện trường đều E một đoạn \(0,6\,\,cm\), từ điểm M đến điểm N dọc theo một đường sức điện thì lực điện sinh công \(9,{6.10^{ - 18}}\,\,J\). Đến N êlectron di chuyển tiếp \(0,4\,\,cm\) từ điểm N đến điểm P theo phương và chiều nói trên. Tính vận tốc của êlectron khi nó đến điểm P. Biết rằng, tại M, êlectron không có vận tốc đầu. Khối lượng của êlectron là \(9,{1.10^{ - 31}}\,\,kg\).
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{A_{MN}} = qE{d_1}}\\{{A_{NP}} = qE{d_2}}\end{array}} \right.\)
\( \Rightarrow \frac{{{A_{NP}}}}{{{A_{MN}}}} = \frac{{{d_2}}}{{{d_1}}} \Rightarrow {A_{NP}} = {A_{MN}}.\frac{{{d_2}}}{{{d_1}}} = 9,{6.10^{ - 18}}.\frac{{0,4}}{{0,6}} = 6,{4.10^{ - 18}}\,\,\left( J \right)\)
Công của lực điện khi electron di chuyển từ điểm M đến điểm P là:
\({A_{MP}} = {A_{MN}} + {A_{NP}} = (9,6 + 6,4){.10^{ - 18}} = {16.10^{ - 18}}\,\,\left( J \right)\)
Theo định lí động năng ta có:
\(\begin{array}{l}
{A_{MP}} = {{\rm{W}}_{dP}} - {{\rm{W}}_{dM}} \Rightarrow {A_{MP}} = \frac{{mv_P^2}}{2} - \frac{{mv_M^2}}{2} \Rightarrow {A_{MP}} = \frac{{mv_P^2}}{2}\\
\Rightarrow {v_P} = \sqrt {\frac{{2{A_{MP}}}}{m}} = \sqrt {\frac{{{{2.16.10}^{ - 18}}}}{{9,{{1.10}^{ - 31}}}}} = 5,{93.10^6}\,\,\left( {m/s} \right)
\end{array}\)
Hướng dẫn giải:
Định lí động năng: Độ biến thiên động năng của một vật bằng công của ngoại lực tác dụng lên vật.
Công của lực điện: \(A = qEd\)
