Câu hỏi:
2 năm trước
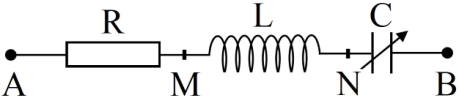
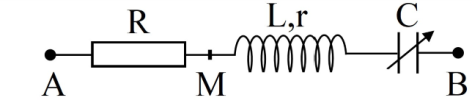Một đoạn mạch \(AB\) gồm hai đoạn mạch \(AM\) và \(MB\) mắc nối tiếp. Đoạn mạch \(AM\) chỉ có biến trở \(R\), đoạn mạch \(MB\) gồm tụ \(C\) mắc nối tiếp với cuộn dây không thuần cảm có độ tự cảm \(L\), điện trở thuần \(r\). Đặt vào \(AB\) một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Điều chỉnh \(R\) đến giá trị \(80\Omega \) thì công suất tiêu thụ trên biến trở đạt cực đại, đồng thời tổng trở của đoạn mạch \(AB\) là số nguyên và chia hết cho \(40\). Khi đó hệ số công suất của đoạn mạch \(MB\) có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: d
Điều chỉnh R đến giá trị \(80\Omega \) thì công suất tiêu thụ trên biến trở cực đại
\( \Rightarrow R = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} {\rm{}} = 80\) (1)
Có tổng trở của đoạn mạch là số nguyên và chia hết cho \(40\)
\( \to {Z_{AB}} = 40n\) (n là số nguyên)
\( \Rightarrow {Z_{AB}} = \sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} {\rm{}} = 40n \Leftrightarrow {\left( {80 + r} \right)^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2}\) (2)
Từ (1) và (2) ta có: \(\left\{ \begin{array}{l}{r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {80^2}\\{\left( {80 + r} \right)^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {80^2}\\{80^2} + 160r + {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2}\end{array} \right. \Rightarrow r = 10{n^2} - 80\)
Hệ số công suất của đoạn MB là: \(c{\rm{os}}{\varphi _{MB}} = \dfrac{r}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{10{n^2} - 80}}{{80}}\)
Có: \(c{\rm{os}}{\varphi _{MB}} \le 1 \Leftrightarrow \dfrac{{10{n^2} - 80}}{{80}} \le 1 \Rightarrow n \le 4\)
+ Với \(n = 4 \to cos{\varphi _{MB}} = 1\)
+ Với \(n{\rm{ }} = {\rm{ }}3 \to c{\rm{os}}{\varphi _{MB}} = \dfrac{{{{10.3}^2} - 80}}{{80}} = 0,125\)
Hướng dẫn giải:
+ Dạng bài Mạch RLC có R biến thiên để \({P_{{R_{max}}}}\) , khi đó: \(R = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Sử dụng biểu thức tính hệ số công suất: \({\rm{cos}}\varphi =\dfrac{R}{Z}\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
