Câu hỏi:
2 năm trước
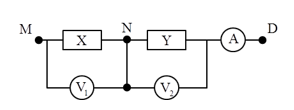
Cho mạch điện như hình vẽ: \(X,{\rm{ }}Y\) là hai hộp, mỗi hộp chỉ chứa $2$ trong $3$ phần tử: điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Ampe kế có điện trở rất nhỏ, các vôn kế có điện trở rất lớn. Các vôn kế và ampe kế đo được cả dòng điện xoay chiều và một chiều. Ban đầu mắc hai điểm $N, D$ vào hai cực của một nguồn điện không đổi thì \({V_2}\) chỉ \(45{\rm{ }}V\), ampe kế chỉ \(1,5{\rm{ }}A\). Sau đó mắc \(M,{\rm{ }}D\) vào nguồn điện xoay chiều có điện áp \(u{\rm{ }} = {\rm{ }}120cos100\pi t{\rm{ }}V\) thì ampe kế chỉ \(1{\rm{ }}A\), hai vôn kế chỉ cùng một giá trị và $u_{MN}$ lệch pha $0,5π $ so với $u_{ND}$. Khi thay tụ $C$ trong mạch bằng tụ $C’$ thì số chỉ vôn kế \({V_1}\) lớn nhất \({U_{1max}}\) . Giá trị \({U_{1max}}\) gần giá trị nào nhất sau đây?
Trả lời bởi giáo viên
Đáp án đúng: b
+ Khi mắc vào hai cực $ND$ một điện áp không đổi $ \to $ có dòng trong mạch với cường độ $I = 1,5{\mkern 1mu} {\mkern 1mu} {\rm{A}} \to $ $ND$ không thể chứa tụ (tụ không cho dòng không đổi đi qua) và ${{\rm{R}}_Y} = \dfrac{{40}}{{1,5}} = 30{\mkern 1mu} {\mkern 1mu} \Omega $
+ Mắc vào hai đầu đoạn mạch $MB$ một điện áp xoay chiều thì ${u_{ND}}$ sớm pha hơn ${u_{MN}}$ một góc \(0,5\pi {\text{}} \to \) X chứa điện trở ${{\rm{R}}_X}$ và tụ điện $C$, $Y$ chứa cuộn dây $L$ và điện trở ${{\rm{R}}_Y}$ .
$ \to $ với ${V_1} = {V_2} \to {U_X} = {U_Y} = 60{\mkern 1mu} {\mkern 1mu} V \to {Z_X} = {Z_Y} = 60{\mkern 1mu} {\mkern 1mu} \Omega $
+ Cảm kháng của cuộn dây ${{\text{Z}}_L} = \sqrt {Z_Y^2 - R_Y^2} {\text{}} = \sqrt {{{60}^2} - {{30}^2}} {\text{}} = 30\sqrt 3 {\mkern 1mu} {\mkern 1mu} \Omega $ .
+ Với ${u_{MN}}$ sớm pha $0,5\pi $ so với ${u_{N{\rm{D}}}}$ và $\tan {\varphi _Y} = \dfrac{{{Z_L}}}{{{R_Y}}} = \dfrac{{30\sqrt 3 }}{{30}} = \sqrt 3 {\text{}} \to {\varphi _Y} = {60^0}$
$ \to {\varphi _X} = {30^0}$
$ \to \left\{ {\begin{array}{*{20}{l}}{{R_X} = 30\sqrt 3 \Omega }\\{{Z_C} = 30\Omega }\end{array}} \right.{\mkern 1mu} {\mkern 1mu} $ .
+ Điện áp hiệu dụng hai đầu $MN$: ${V_1} = {U_{MN}} = \dfrac{{U\sqrt {R_X^2 + Z_C^2} }}{{\sqrt {{{\left( {{R_X} + {R_Y}} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{60\sqrt 2 \sqrt {{{\left( {30\sqrt 3 } \right)}^2} + Z_C^2} }}{{\sqrt {{{\left( {30\sqrt 3 {\text{}} + 30} \right)}^2} + {{\left( {30\sqrt 3 - {Z_C}} \right)}^2}} }}$
+ Sử dụng bảng tính Mode $ \to $ $7$ trên Casio ta tìm được ${V_{1\max }}$ có giá trị lân cận \(75V\)
Hướng dẫn giải:
+ Sử dụng phương pháp giải bài toán hộp đen
+ Áp dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
+ Áp dụng biểu thức: \(Z = \dfrac{U}{I}\)
+ Vận dụng biểu thức: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
