Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với phương thẳng đứng một góc α, có \(\tan \alpha = \dfrac{3}{4}\); lúc này con lắc dao động nhỏ với chu kỳ T1. Nếu đổi chiều điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không đổi thì chu kỳ dao động nhỏ của con lắc lúc này là:
Trả lời bởi giáo viên
Khi vecto cường độ điện trường nằm ngang:
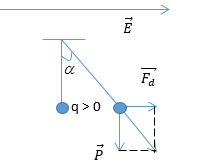
Từ hình vẽ ta có: \(\tan \alpha = \dfrac{{{F_d}}}{P} = \dfrac{{ma}}{{mg}} = \dfrac{3}{4} \Rightarrow a = \dfrac{3}{4}.g\)
Gia tốc trọng trường hiệu dụng :
\(g' = \sqrt {{g^2} + {a^2}} = \sqrt {{g^2} + \dfrac{{9{g^2}}}{{16}}} = \dfrac{5}{4}.g\)
Chu kì dao động của con lắc khi đó:
\({T_1} = 2\pi \sqrt {\dfrac{l}{{g'}}} = \dfrac{2}{{\sqrt 5 }}.2\pi \sqrt {\dfrac{l}{g}} \,\,\,\,\left( 1 \right)\)
+ Khi đổi chiều điện trường sao cho hướng vecto cường độ điện trường hướng lên thì \(\overrightarrow {{F_d}} \) hướng lên (do q > 0). Gia tốc trọng trường hiệu dụng khi đó:
\(g'' = g - a = g - \dfrac{3}{4}.g = \dfrac{1}{4}.g\)
Chu kì dao động của con lắc khi đó:
\({T_2} = 2\pi \sqrt {\dfrac{l}{{g''}}} = 2.2\pi \sqrt {\dfrac{l}{g}} \,\,\,\,\,\left( 2 \right)\)
+ Từ (1) và (2) ta có: \(\dfrac{{{T_2}}}{{{T_1}}} = \sqrt 5 \Rightarrow {T_2} = \sqrt 5 .{T_1}\)
Hướng dẫn giải:
\(\begin{array}{l}\overrightarrow {{F_d}} = q.\overrightarrow E = m.\overrightarrow a \\\overrightarrow {{F_d}} \bot \overrightarrow P \Rightarrow g' = \sqrt {{g^2} + {a^2}} \\\overrightarrow {{F_d}} \uparrow \uparrow \overrightarrow P \Rightarrow g' = g + a\\\overrightarrow {{F_d}} \uparrow \downarrow \overrightarrow P \Rightarrow g' = g - a\\T = 2\pi \sqrt {\dfrac{l}{{g'}}} \end{array}\)

