Câu hỏi:
2 năm trước
Một con lắc đơn dao động điều hòa với chu kì T tại nơi có thêm trường ngoại lực có độ lớn F theo phương ngang. Nếu quay phương của ngoại lực một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) trong mặt phẳng thẳng đứng và giữ nguyên độ lớn thì chu kì dao động là \({T_1} = 2,5\,\,s\) hoặc \({T_2} = 1,6\,\,s\). Chu kì T gần nhất giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: a
Nhận xét: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \Rightarrow {T^2} = 4{\pi ^2}\dfrac{{\rm{l}}}{g} \Rightarrow {T^2} \sim \dfrac{1}{g}\) hay \(g \sim \dfrac{1}{{{T^2}}}\)
Ban đầu \(\overrightarrow F \) theo phương ngang, gia tốc hiệu dụng: \({g_0} = \sqrt {{g^2} + {a^2}} \)
Trường hợp 1: \(\overrightarrow F \) hướng lên trên:
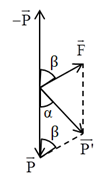
Ta có: \(\beta = {90^0} - \alpha \Rightarrow \cos \beta = - \sin \alpha \)
Gia tốc hiệu dụng là: \({g_1} = \sqrt {{g^2} + {a^2} + 2g.a.\sin \alpha } \)
\( \Rightarrow {g_1}^2 = {g^2} + {a^2} + 2g.a.\sin \alpha \,\,\left( 1 \right)\)
Trường hợp 2: \(\overrightarrow F \) hướng xuống dưới:
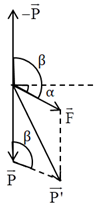
Ta có: \(\beta = {90^0} + \alpha \Rightarrow \cos \beta = \sin \alpha \)
Gia tốc hiệu dụng là: \({g_2} = \sqrt {{g^2} + {a^2} - 2g.a.\sin \alpha } \)
\( \Rightarrow {g_2}^2 = {g^2} + {a^2} - 2g.a.\sin \alpha \,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \({g_1}^2 + {g_2}^2 = 2\left( {{g^2} + {a^2}} \right)\)
\( \Rightarrow \dfrac{1}{{{T_1}^4}} + \dfrac{1}{{{T_2}^4}} = \dfrac{2}{{{T_0}^4}} \Rightarrow \dfrac{1}{{2,{5^4}}} + \dfrac{1}{{1,{6^4}}} = \dfrac{2}{{{T_0}^4}} \Rightarrow {T_0} \approx 1,83\,\,\left( s \right)\)
Hướng dẫn giải:
Gia tốc hiệu dụng của con lắc khi ngoại lực hướng theo phương ngang: \({g_0} = \sqrt {{g^2} + {a^2}} \)
Gia tốc hiệu dụng của con lắc khi ngoại lực hợp với phương thẳng đứng góc β:
\(g' = \sqrt {{g^2} + {a^2} - 2g.a.cos\beta } \)
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
