Câu hỏi:
2 năm trước
Một cái thước được cắm thẳng đứng vào bình nước có đáy phẳng, ngang. Phần thước nhô khỏi mặt nước là \(4cm\). Chếch ở trên có một ngọn đèn. Bóng của thước trên mặt nước dài \(4cm\) và ở đáy dài \(8cm\). Tính chiều sâu của nước trong bình. Biết chiết suất của nước là \(\dfrac{4}{3}\).
Trả lời bởi giáo viên
Đáp án đúng: c
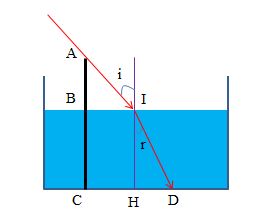
+ Theo đề bài, ta có:
Thước AC
- Phần thước nhô khỏi mặt nước: \(AB = {\rm{ }}4cm\)
- Bóng của thước trên mặt nước: \(BI{\rm{ }} = {\rm{ }}4cm\)
- Bóng của thước ở đáy: \(CD = {\rm{ }}8cm\)
- Chiều sâu của nước trong bình: \(BC = IH\)
+ Lại có:
\(\begin{array}{l}CD = CH + HD\\ \Rightarrow HD = CD - CH = 8 - 4 = 4cm\end{array}\)
+ Xét \(\Delta ABI\), có
\(AB = BI\) \( \Rightarrow \Delta ABI\) vuông cân tại B
Ta suy ra \(\widehat {BAI} = \widehat {BIA} = i = {45^0}\)
+ Áp dụng định luật khúc xạ ánh sáng ta có:
\(\begin{array}{l}\sin i = n\sin r \Leftrightarrow \sin {45^0} = \dfrac{4}{3}{\rm{sinr}}\\ \Rightarrow {\rm{sinr}} = \dfrac{3}{4}\sin {45^0} = \dfrac{{3\sqrt 2 }}{8}\\ \Rightarrow r = {32^0}\end{array}\)
+ Xét \(\Delta IHD\), có:
\(\begin{array}{l}\tan \widehat {HID} = {\mathop{\rm t}\nolimits} {\rm{anr}} = \dfrac{{HD}}{{IH}}\\ \Rightarrow IH = \dfrac{{HD}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \dfrac{4}{{\tan {{32}^0}}} \approx 6,4cm\end{array}\)
Hướng dẫn giải:
+ Sử dụng hệ thức lượng trong tam giác
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
