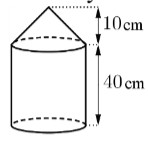
Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ ghép lại). Chiều cao đo được ghi trên hình, chu vi đáy là \(20\sqrt 3 \pi \) cm. Thể tích của cột bằng:
Trả lời bởi giáo viên
Gọi \(r\) là bán kính đường tròn đáy của hình trụ và hình nón.
Theo bài ra ta có: Chu vi đáy là \(C = 2\pi r = 20\sqrt 3 \pi \Rightarrow r = 10\sqrt 3 \,\,\left( {cm} \right)\)
Thể tích khối nón là \({V_1} = \dfrac{1}{3}\pi {r^2}.{h_1} = \dfrac{1}{3}\pi .{\left( {10\sqrt 3 } \right)^2}.10 = 1000\pi \,\,\left( {c{m^3}} \right)\)
Thể tích khối trụ là \({V_2} = \pi {r^2}.{h_2} = \pi .{\left( {10\sqrt 3 } \right)^2}.40 = 12000\pi \,\,\,\left( {c{m^3}} \right)\)
Thể tích của cột là \(V = {V_1} + {V_2} = 13000\pi \,\,\left( {c{m^3}} \right)\).
Hướng dẫn giải:
- Chu vi đường tròn bán kính \(R\) là \(C = 2\pi R\).
- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).
- Thể tích khối trụ có chiều cao \(h\), bán kính đáy \(r\) là \(V = \pi {r^2}h\).

