Cho khối trụ có hai đáy là hình tròn \(\left( {O;R} \right)\) và \(\left( {O';R} \right)\), \(OO' = 4R\). Trên đường tròn tâm $O$ lấy \(\left( O \right)\) lấy hai điểm $A, B$ sao cho \(AB = R\sqrt 3 \). Mặt phẳng $(P) $ đi qua $A, B$ cắt $OO’$ và tạo với đáy một góc bằng $60^0$. $(P)$ cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng:

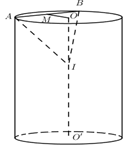
Gọi $M $ là trung điểm của $AB$ ta có:

\(OM = \sqrt {O{A^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}}  = \sqrt {{R^2} - \dfrac{{3{R^2}}}{4}}  = \dfrac{R}{2}\)

Giả sử mặt phẳng (P) cắt trục OO’ tại I. Ta có : IA = IB nên \(\Delta IAB\) cân tại I, do đó \(MI \bot AB\)

Do đó góc giữa (P) và mặt đáy bằng \(\widehat {IMO} = {60^0}\)

Xét tam giác vuông IMO có : \(OI = OM.\tan 60 = \dfrac{{R\sqrt 3 }}{2} < \dfrac{{OO'}}{2} = 2R\)

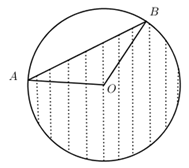
\( \Rightarrow I\) nằm giữa O và O’. Do đó (P) không cắt đáy còn lại.Vậy hình chiếu của (P) trên \(\left( {O;R'} \right)\) là phần diện tích của hình quạt cung lớn AB và \(\Delta OAB\)(phần gạch chéo).

Áp dụng định lí Cosin trong tam giác OAB có :

\(\cos \widehat {AOB} = \dfrac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \dfrac{{{R^2} + {R^2} - 3{R^2}}}{{2{R^2}}} =  - \dfrac{1}{2} \Rightarrow \widehat {AOB} = {120^0}\)

\( \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}OA.OB.\sin 120 = \dfrac{1}{2}{R^2}\dfrac{{\sqrt 3 }}{2} = {R^2}\dfrac{{\sqrt 3 }}{4}\)

Gọi ${{S}_{\overset\frown{OAB}}}$ là diện tích hình quạt $\Rightarrow {{S}_{\overset\frown{OAB}}}=\dfrac{\dfrac{4\pi }{3}}{2\pi }.\pi {{R}^{2}}=\dfrac{2}{3}\pi {{R}^{2}}$

$\Rightarrow {{S}_{hc}}={{S}_{\overset\frown{OAB}}}+{{S}_{\Delta OAB}}=\dfrac{2}{3}\pi {{R}^{2}}+{{R}^{2}}\dfrac{\sqrt{3}}{4}$  

Vậy diện tích phần thiết diện cần tìm là :

${S_{hc}} = S.\cos 60 \Rightarrow S = \dfrac{{{S_{hc}}}}{{\cos 60}} = 2\left( {\dfrac{2}{3}\pi {R^2} + {R^2}\dfrac{{\sqrt 3 }}{4}} \right) = \left( {\dfrac{4}{3}\pi {R^2} + \dfrac{{\sqrt 3 }}{2}{R^2}} \right) = \left( {\dfrac{4}{3}\pi  + \dfrac{{\sqrt 3 }}{2}} \right){R^2}$