Câu hỏi:
2 năm trước
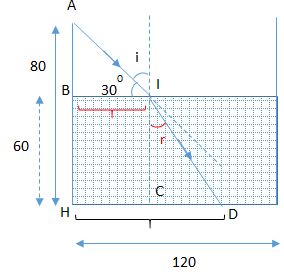
Một bể chứa nước có thành cao \(80{\rm{ }}cm\) và đáy phẳng dài \(120{\rm{ }}cm\) và độ cao mực nước trong bể là \(60{\rm{ }}cm\), chiết suất của nước là \(\dfrac{4}{3}\). Ánh nắng chiếu theo phương nghiêng góc \({30^0}\) so với phương ngang.
Độ dài bóng đen tạo thành trên đáy bể là:
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \(\dfrac{{{\rm{Sin i}}}}{{{\rm{Sin r}}}} = {\rm{n = }}\dfrac{4}{3} = > {\mathop{\rm sinr}\nolimits} = \dfrac{3}{4}.\sin i\)
Mà \(i = {90^0} - {30^0} = {60^0}\)=> \({\mathop{\rm sinr}\nolimits} = \dfrac{3}{4}.\sin i = \dfrac{3}{4}.\sin {60^0} = \dfrac{{3\sqrt 3 }}{8} = > r = {40,51^0}\)
Xét tam giác vuông ICD có \(CD = IC.\tan r = BH.\tan r = 60.\tan r = 60.\tan {40,51^0} = 51,25\)
=> Độ dài bóng đen tạo thành trên đáy bể là HD= HC + CD = BI + CD = 34,6 + 51,25 = 85,85 cm
Hướng dẫn giải:
Vẽ hình, sử dụng định luật khúc xạ ánh sáng và hệ thức lượng giác trong tam giác vuông
- Độ dài bóng đen tạo thành trên đáy bể là HD
- HD = HC + CD = BI + CD
- Tính CD: xét tam giác vuông ICD có \(CD = IC.{\mathop{\rm tanr}\nolimits} = BH.{\mathop{\rm tanr}\nolimits} = 60.{\mathop{\rm tanr}\nolimits} \)
- Tính r: sử dụng ĐL KXAS: \(\dfrac{{{\rm{Sin i}}}}{{{\rm{Sin r}}}} = {\rm{n = }}\dfrac{4}{3}\)
Với \(i = {90^0} - {30^0} = {60^0}\), tính được r => CD
=> HD
