Câu hỏi:
2 năm trước
Một bản mặt song song có bề dày \(10{\rm{ }}cm\), chiết suất \(n{\rm{ }} = {\rm{ }}1,5\) được đặt trong không khí. Chiếu tới bản một tia sáng \(SI\) có góc tới \({45^0}\)
Khoảng cách giữa tia tới và tia ló là:
Trả lời bởi giáo viên
Đáp án đúng: c
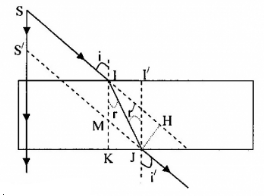
- Gọi d là khoảng cách giữa giá của tia tới và tia ló, d = JH
- Xét tam giác vuông IJH: \(JH = {\rm{IJ}}.\sin (i - r)\)
- Xét tam giác vuông IJK: \({\rm{IJ = }}\dfrac{{IK}}{{{\mathop{\rm cosr}\nolimits} }} = \dfrac{e}{{\cos r}}\)
=> \(d = JH = \dfrac{e}{{c{\rm{osr}}}}.\sin (i - r)\)
- Tính r:
Áp dụng định luật khúc xạ ánh sáng có: \(\sin i = n.\sin r \to \sin {45^0} = 1,5.sin{\rm{r}} \to r = {28,13^0}\)
- Thay số tính d: với e = 10 cm
=> \(d = JH = \dfrac{{10}}{{c{\rm{os(28}}{\rm{,13)}}}}.\sin (45 - 28,13) = 3,29cm\)
Hướng dẫn giải:
Sử dụng công thức tính khoảng cách giữa giá của tia ló và tia tới qua bản mặt song song:
\(d = \dfrac{e}{{c{\rm{osr}}}}.\sin (i - r)\) trong đó: e là bề dày của bản mặt song song
