Câu hỏi:
2 năm trước
Mạch điện xoay chiều nối tiếp AB theo đúng thứ tự gồm cuộn cảm thuần L, điện trở thuần R và tụ điện C. Cho biết điện áp hiệu dụng \({U_{RL}} = {U_{RC}}\sqrt 3 \) và R2 = L/C. Tính hệ số công suất của đoạn mạch AB.
Trả lời bởi giáo viên
Đáp án đúng: c
Theo đầu bài, ta có:
\(\begin{array}{l}{R^2} = \dfrac{L}{C} = \omega L\dfrac{1}{{\omega C}} = {Z_L}{Z_C}\\ \to \dfrac{{{Z_L}}}{R}\dfrac{{\left( { - {Z_L}} \right)}}{R} = - 1\\ \to \tan {\varphi _{RL}}\tan {\varphi _{RC}} = - 1\\ \Rightarrow {u_{RL}} \bot {u_{RC}}\end{array}\)
Vẽ giản đồ véctơ, ta được:
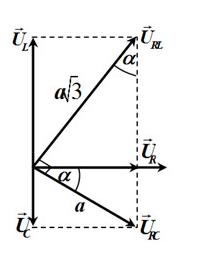
Từ giản đồ véctơ, ta có:
\(\begin{array}{l}\tan \alpha = \dfrac{{{U_{RC}}}}{{{U_{RL}}}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }} \to \alpha = {30^0}\\\left\{ \begin{array}{l}{U_R} = ac{\rm{os}}\alpha = \dfrac{{a\sqrt 3 }}{2}\\{U_C}{\rm{ = asin}}\alpha = \dfrac{a}{2}\\{U_L} = a\sqrt 3 {\rm{cos}}\alpha = \dfrac{{3a}}{2}\end{array} \right. \\\to c{\rm{os}}\varphi {\rm{ = }}\dfrac{{{U_R}}}{U} = \dfrac{{{U_R}}}{{\sqrt {{U_R}^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} }} = \sqrt {\dfrac{3}{7}} \end{array}\)
Hướng dẫn giải:
Sử dụng giản đồ véctơ
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
