Câu hỏi:
2 năm trước
Hai vật \({m_1} = 5kg,{m_2} = 10kg\) được nối với nhau bằng một dây nhẹ, đặt trên mặt phẳng nằm ngang không ma sát. Tác dụng nằm ngang \(F = 18N\) lên vật \({m_1}\).
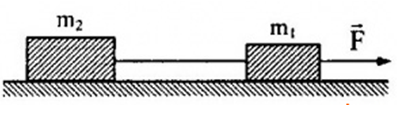
Quãng vật đường vật đi được sau 2s là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có:
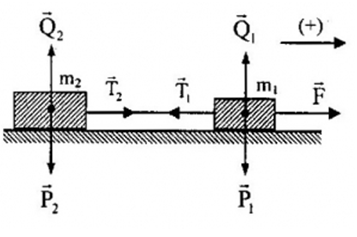
- Các lực tác dụng lên vật \({m_1}\): trọng lực \(\overrightarrow {{P_1}} \), phản lực \(\overrightarrow {{Q_1}} \) của mặt sàn, lực kéo \(\overrightarrow F \) , lực căng \(\overrightarrow {{T_1}} \) của dây.
- Các lực tác dụng lên vật \({m_2}\): trọng lực \(\overrightarrow {{P_2}} \), phản lực \(\overrightarrow {{Q_2}} \) của mặt sàn , lực căng \(\overrightarrow {{T_2}} \) của dây.
- Theo định luật II - Niutơn, ta có:
+ Vật \({m_1}\): \(\overrightarrow {{P_1}} + \overrightarrow {{Q_1}} + \overrightarrow F + \overrightarrow {{T_1}} = {m_1}\overrightarrow {{a_1}} \) (1)
+ Vật \({m_2}\): \(\overrightarrow {{P_2}} + \overrightarrow {{Q_2}} + \overrightarrow {{T_2}} = {m_2}\overrightarrow {{a_2}} \) (2)
Chiếu (1) và (2) lên phương ngang, theo chiều chuyển động của mỗi vật, ta được:
\(\left\{ \begin{array}{l}F - {T_1} = {m_1}{a_1}{\rm{ }}\left( a \right)\\{T_2} = {m_2}{a_2}{\rm{ }}\left( b \right)\end{array} \right.\)
- Vì \(\left\{ \begin{array}{l}{T_1} = {T_2}\\{a_1} = {a_2} = a\end{array} \right.\) nên từ \(\left( a \right) + \left( b \right)\) , ta suy ra: \(F = \left( {{m_1} + {m_2}} \right)a\)
\( \to a = \frac{F}{{{m_1} + {m_2}}} = \frac{{18}}{{5 + 10}} = 1,2m/{s^2}\)
=> Quãng đường vật đi được sau 2s là: \(s = \frac{1}{2}a{t^2} = \frac{1}{2}.1,{2.2^2} = 2,4m\)
Hướng dẫn giải:
+ Xác định các ngoại lực tác dụng lên hệ thang máy và vật m
+ Viết phương trình định luật II - Niutơn cho từng vật
+ Chiếu phương trình định luật II của mỗi vật lên chiều đã chọn
+ Vận dụng phương trình: \(s = \frac{1}{2}a{t^2}\)
