Câu hỏi:
2 năm trước
Hai tiếp tuyến tại hai điểm $B,C$ của một đường tròn $\left( O \right)$ cắt nhau tại $A$ tạo thành \(\widehat {BAC} = {50^0}\). Số đo của góc \(\widehat {BOC}\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
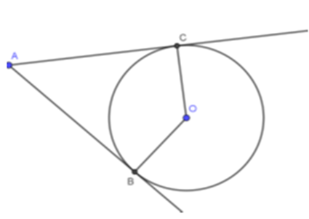
Vì hai tiếp tuyến của đường tròn $\left( O \right)$ cắt nhau tại $A$ nên \(\widehat {ACO} = \widehat {ABO} = {90^0} \Rightarrow \widehat {CAB} + \widehat {COB} = {360^0} - {180^0} = {180^0}\)
Mà \(\widehat {CAB} = {50^0}\) nên \(\widehat {COB} = {180^0} - {50^0} = {130^0}\)
Hướng dẫn giải:
Sử dụng tính chất tiếp tuyến
Sử dụng định lý "tổng bốn góc trong một tứ giác là $360^0$ "