Câu hỏi:
2 năm trước
Hai tiếp tuyến tại $A$ và $B$ của đường tròn $\left( {O;R} \right)$ cắt nhau tại $M.$ Nếu $MA = \;R\sqrt 3 $ thì góc $\widehat {AOB}$ bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
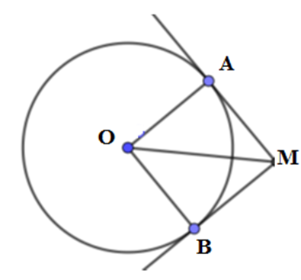
Có $AM$ là tiếp tuyến của đường tròn $\left( O \right)$ nên $AM$ vuông góc với $OA$
Xét tam giác $AOM$ vuông tại $A$ nên có $\tan \widehat {AOM} = \dfrac{{AM}}{{OA}} = \dfrac{{R\sqrt 3 }}{R} = \sqrt 3 $$ \Rightarrow \widehat {AOM} = {60^0}$
Mà hai tiếp tuyến $AM$ và $BM$ cắt nhau tại $M$ nên ta có $OM$ là phân giác của $\widehat {AOB}$
Vậy $\widehat {AOB}$$ = 2\widehat {AOM} = {2.60^0} = {120^0}$
Hướng dẫn giải:
Tính chất hai tiếp tuyến cắt nhau và tỉ số lượng giác của góc nhọn.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
