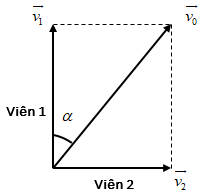
Hai hòn bi có khối lượng bằng nhau đặt trên một mặt bàn nhẵn. Hòn bi 1 chuyển động với vận tốc \({v_0}\) đến đập vào hòn bi 2 đang đứng yên. Sau va chạm chúng chuyển động theo hai hướng vuông góc với nhau với các tốc độ \({v_1} = 4m/s\) và \({v_2} = 3m/s\). Tính \({v_0}\) và hướng lệch của hòn bi 1.
Trả lời bởi giáo viên
Áp dụng định luật II Niuton cho:
Viên bi 1: \(\overrightarrow {{F_{21}}} = {m_1}\overrightarrow {{a_1}} = {m_1}.\dfrac{{\overrightarrow {{v_1}} - \overrightarrow {{v_0}} }}{{\Delta t}} = m.\dfrac{{\overrightarrow {{v_1}} - \overrightarrow {{v_0}} }}{{\Delta t}}\)
Viên bi 2: \(\overrightarrow {{F_{12}}} = {m_2}\overrightarrow {{a_2}} = {m_2}.\dfrac{{\overrightarrow {{v_2}} - \overrightarrow 0 }}{{\Delta t}} = m.\dfrac{{\overrightarrow {{v_2}} - \overrightarrow 0 }}{{\Delta t}}\)
Áp dụng định luật III Niuton ta có: \(\overrightarrow {{F_{21}}} = - \overrightarrow {{F_{12}}} \Leftrightarrow \overrightarrow {{v_1}} - \overrightarrow {{v_0}} = - \overrightarrow {{v_2}} \Rightarrow \overrightarrow {{v_0}} = \overrightarrow {{v_1}} + \overrightarrow {{v_2}} \,\,\left( * \right)\)
Áp dụng quy tắc hình bình hành ta có:
Vì \(\overrightarrow {{v_1}} \bot \overrightarrow {{v_2}} \Rightarrow {v_0} = \sqrt {v_1^2 + v_2^2} = \sqrt {{4^2} + {3^2}} = 5m/s\)
Có: \(\sin \alpha = \dfrac{{{v_2}}}{{{v_0}}} = \dfrac{3}{5} \Rightarrow \alpha \approx 36,{87^0}\)
Hướng dẫn giải:
+ Định luật II Niuton: Gia tốc của một vật cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật.
Biểu thức: \(\overrightarrow a = \dfrac{{\overrightarrow F }}{m} \Rightarrow \overrightarrow F = m\overrightarrow a \)
+ Định luật III Niuton: Trong mọi trường hợp, khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng lên vật A một lực. Hai lực này có cùng giá, cùng độ lớn, nhưng ngược chiều.
\(\overrightarrow {{F_{BA}}} = - \overrightarrow {{F_{AB}}} \)