Hai chất điểm có khối lượng \({m_1} = 2{m_2}\)dao động điều hòa trên hai đường thẳng song song, sát nhau với biên độ bằng nhau và bằng \(8 cm\), vị trí cân bằng của chúng nằm sát nhau. Tại thời điểm \({t_0}\), chất điểm \({m_1}\) chuyển động nhanh dần qua li độ \(4\sqrt 3cm\), chất điểm \({m_2}\) chuyển động ngược chiều dương qua vị trí cân bằng. Tại thời điểm t, chúng gặp nhau lần đầu tiên trong trạng thái chuyển động ngược chiều nhau qua li độ \(x = - 4 cm\). Tỉ số động năng của chất điểm thứ nhất so với chất điểm thứ hai tại thời điểm gặp nhau lần thứ \(2019\) là
Trả lời bởi giáo viên
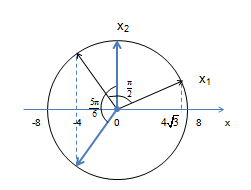
Biểu diễn dao động của hai chất điểm trên vòng tròn lượng giác:
Khi hai chất điểm gặp nhau:
\(\left\{ \begin{array}{l}{\omega _1}\Delta t = \dfrac{\pi }{2}\\{\omega _2}\Delta t = \dfrac{{5\pi }}{6}\end{array} \right. \to \dfrac{{{\omega _1}}}{{{\omega _2}}} = \dfrac{3}{5}\)
+ Tỉ số động năng của chất điểm thứ nhất so với chất điểm thứ hai tại thời điểm gặp nhau lần thứ n = 2019 (hoặc lần gặp nhau thứ n bất kỳ) là : \(\dfrac{{{{\rm{W}}_{d1}}}}{{{{\rm{W}}_{d2}}}} = \dfrac{{\dfrac{1}{2}{m_1}v_1^2}}{{\dfrac{1}{2}{m_2}v_2^2}} = \dfrac{{2{m_2}.\omega _1^2({A^2} - \overbrace {x_1^2}^{{x_1} = {x_2}})}}{{{m_2}.\omega _2^2({A^2} - x_2^2)}} = 2.{\left( {\dfrac{3}{5}} \right)^2} = 0,72\)
Hướng dẫn giải:
Sử dụng vòng tròn lượng giác
Động năng của con lắc: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m.{\omega ^2}({A^2} - {x^2})\)

