Câu hỏi:
3 năm trước
Giá trị nguyên có thể có của $m$ để $2$ đường thẳng $d:y = mx - 2;d':y = 2x + 1$ cắt nhau tại điểm có hoành độ là số nguyên.
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: $d \cap d' \Leftrightarrow m \ne 2$.
Xét phương trình hoành độ giao điểm của $d$ và $d'$: $mx - 2 = 2x + 1 \Leftrightarrow (m - 2)x = 3 \Leftrightarrow x = \dfrac{3}{{m - 2}}$
Ta có: $x = \dfrac{3}{{m - 2}} \in Z \Leftrightarrow m - 2 \in U(3) = \left\{ { \pm 1; \pm 3} \right\}$.
Ta có bảng sau:
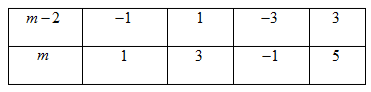
Vậy $m \in \left\{ { - 1;1;3;5} \right\}$.
Hướng dẫn giải:
- Điều kiện để 2 đường thẳng cắt nhau.
- Tìm tọa độ giao điểm 2 đường thẳng.
- Tìm nghiệm nguyên.

