Câu hỏi:
2 năm trước
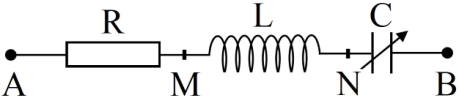
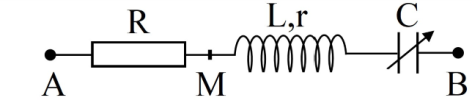Đoạn mạch $AB$ được mắc nối tiếp theo thứ tự, cuộn dây với hệ số tự cảm $L = \dfrac{2}{{5\pi }}H$ , biến trở $R$ và tụ điện có điện dung $C = \dfrac{{{{10}^{ - 2}}}}{{25\pi }}F$. Điểm $M$ là điểm nối giữa $R$ và $C$. Nếu mắc vào hai đầu $A, M$ một ắc quy có suất điện động $12V$ và điện trở trong $4\Omega $ điều chỉnh $R = {R_1}$ thì có dòng điện cường độ $0,1875A$. Mắc vào $AB$ một hiệu điện thế $u = 120\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)\left( V \right)$ rồi điều chỉnh $R = {R_2}$ thì công suất tiêu thụ trên biến trở đạt cực đại bằng $160W$. Tỷ số ${R_1}:{R_2}$ là:
Trả lời bởi giáo viên
Đáp án đúng: a
Giả sử cuộn dây thuần cảm:
Ta có, khi \(R{\rm{ }} = {\rm{ }}{R_2}\) công suất tiêu thụ trên biến trở cực đại.
Khi đó ta có: \({R_2} = \left| {{Z_L} - {Z_C}} \right| = 40 - 25 = 15W\)
Mặt khác: \({P_{{R_2}}} = \dfrac{{{U^2}}}{{2{R_2}}} = \dfrac{{{{120}^2}}}{{2.15}} = 480 \ne 160\)
=> điều giả sử ban đầu là sai
=> Cuộn dây không thuần cảm có điện trở $r$
- Ta có:
+ Ban đầu khi mắc vào hai đầu $A, M$ một ắc quy có suất điện động \(E{\rm{ }} = {\rm{ }}12V\), điện trở trong \({r_1} = 4\Omega \) thì \({I_1} = 0,1875\)
Theo định luật Ôm, ta có: \({I_1} = \dfrac{E}{{{R_b} + r}} = \dfrac{E}{{{R_1} + r + {r_1}}} \to {R_1} + {r_1} + r = \dfrac{E}{{{I_1}}} = 64 \to {R_1} + r = 60\Omega {\rm{}}({\rm{1}})\)
+ Khi mắc vào A,B một hiệu điện thế \(u = 120\sqrt 2 {\rm{cos100}}\pi {\rm{t}}\) ,\(R = {R_2}\) thì công suất tiêu thụ trên biến trở cực đại và bằng \(160W\)
Ta có: Công suất trên biến trở R đạt cực đại khi \({R_2}^2 = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2}{\rm{ }}({\rm{2}})\)
Mặt khác, ta có: Công suất trên \({R_2}\):
\(\begin{array}{l}P{\rm{ = }}\dfrac{{{U^2}}}{{{{({R_2} + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R_2} = 160{\rm{W}}\\ \to \dfrac{{{R_2}}}{{{{({R_2} + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \dfrac{{160}}{{{{120}^2}}} = \dfrac{1}{{90}}90\\{R_2} = 2R_2^2 + 2{\rm{r}}R \to {R_2} + r = 45\end{array}\)
Kết hợp với (2) ta được: \(R_2^2 = {(45 - {R_2})^2} + {15^2} \to {R_2} = 25\Omega ,r = 20\Omega \)
Với \(r = 20\Omega \) thay vào (1) \( \to {R_1} = 60 - 20 = 40\Omega \)
\( \to \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{40}}{{25}} = 1,6\)
Hướng dẫn giải:
Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
