Câu hỏi:
2 năm trước
Điền số thích hợp vào ô trống:
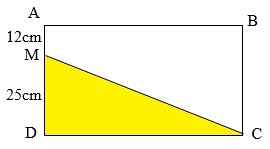
Cho hình vẽ như bên dưới:
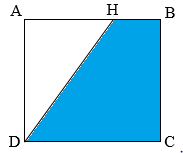
Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\).
Vậy diện tích hình thang \(HBCD\) là
\(d{m^2}\).
Trả lời bởi giáo viên
Đáp án:
Cho hình vẽ như bên dưới:
Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\).
Vậy diện tích hình thang \(HBCD\) là
\(d{m^2}\).
Ta có \(50 \times 50 = 2500\). Vậy độ dài cạnh hình vuông \(ABCD\) là \(50dm\) hay \(AB = BC = CD = AD = 50dm\).
Ta có \(HBCD\) là hình thang vuông với chiều cao là cạnh \(BC\), hai đáy là \(HB,\,\,DC\).
Độ dài cạnh \(AH\) là:
\(50:100 \times 70 = 35\;(dm)\)
Độ dài cạnh \(HB\) là:
\(50 - 35 = 15\;(dm)\)
Diện tích hình thang \(HBCD\) là:
\((15 + 50) \times 50:2 = 1625\;(d{m^2})\)
Đáp số: \(1625d{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(1625\).
Hướng dẫn giải:
- Tìm độ dài cạnh hình vuông.
- Tìm độ dài các cạnh đáy và chiều cao của hình thang sau đó để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho \(2\).
Câu hỏi khác
Câu 1:
.jpg)
78
