Câu hỏi:
2 năm trước
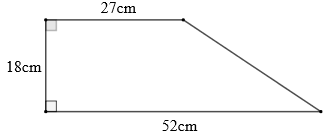
Điền số thích hợp vào chỗ trống:
Cho hình chữ nhật $ABCD$ có $AB = 24,4cm\;;{\rm{ }}BC = 11cm\;$.
Điểm \(M\) nằm trên cạnh $AB$ sao cho$AM = \dfrac{3}{5}AB$.
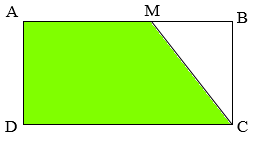
Diện tích hình thang $AMCD$ là
\(c{m^2}\)
Trả lời bởi giáo viên
Đáp án:
Cho hình chữ nhật $ABCD$ có $AB = 24,4cm\;;{\rm{ }}BC = 11cm\;$.
Điểm \(M\) nằm trên cạnh $AB$ sao cho$AM = \dfrac{3}{5}AB$.
Diện tích hình thang $AMCD$ là
\(c{m^2}\)
Vì $ABCD$ là hình chữ nhật nên $AB = CD = 24,4cm;\,\,AD = BC = 11cm$.
Hình thang $AMCD$ có chiều cao là \(AD = 11cm\).
Độ dài cạnh \(AM\) là:
\(24,4 \times \dfrac{3}{5} = 14,64\;(cm)\)
Diện tích hình thang $AMCD$ là:
\(\dfrac{{(14,64 + 24,4) \times 11}}{2} = 214,72\;\left( {c{m^2}} \right)\)
Đáp số: \(214,72c{m^2}\).
Hướng dẫn giải:
- $ABCD$ là hình chữ nhật nên $AB = CD = 24,4cm;\,\,AD = BC = 11cm$
- Tính độ dài cạnh \(AM\) ta lấy độ dài cạnh \(AB\) nhân với \(\dfrac{3}{5}\).
- Hình thang $AMCD$ có chiều cao chính là cạnh \(AD\), từ đó tính diện tích hình thang theo công thức:
\(S = (AM + CD) \times AD:2\).
Trong các hình sau, hình nào là hình thang?
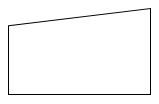
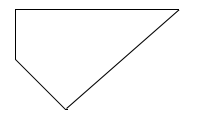
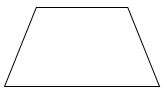
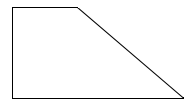
Điền số thích hợp vào ô trống:
