Câu hỏi:
3 năm trước
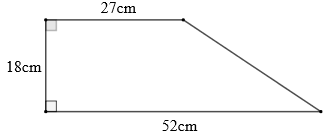
Hình thang $ABCD$ có chiều cao $AH$ bằng $75cm$; đáy bé bằng $\dfrac{2}{3}$ đáy lớn. Biết diện tích hình thang bằng diện tích hình chữ nhật có chiều dài $135cm$; chiều rộng $50cm$. Tính độ dài đáy lớn, đáy bé của hình thang.
Trả lời bởi giáo viên
Đáp án đúng:
D. Đáy lớn \(108cm\) ; đáy bé \(72cm\)
Diện tích hình chữ nhật là:
\(135 \times 50 = 6750\;(c{m^2})\)
Vậy hình thang có diện tích là \(6750c{m^2}\).
Tổng độ dài hai đáy của hình thang là:
\(6750 \times 2:75 = 180\;(cm)\)
Ta có sơ đồ
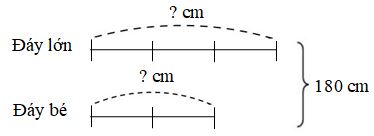
Theo sơ đồ, tổng số phần bằng nhau là:
\(2 + 3 = 5\) (phần)
Giá trị một phần là:
\(180:5 = 36\;(cm)\)
Độ dài đáy lớn là:
\(36 \times 3 = 108\;(cm)\)
Độ dài đáy bé là:
\(180 - 108 = 72\;(cm)\)
Đáp số: Đáy lớn \(108cm\) ; đáy bé \(72cm\).
Hướng dẫn giải:
- Tính diện tích hình chữ nhật theo công thức: Diện tích = chiều dài × chiều rộng.
Từ đó tìm được diện tích hình thang.
- Từ công thức tính diện tích \(S = \dfrac{{(a + b) \times h}}{2}\) ta có thể tính tổng độ dài hai đáy \(h\) theo công thức \(a + b = \dfrac{{S \times 2}}{h}\) hoặc \(a + b = S \times 2:h\).
Khi đó ta có bài toán tổng tỉ cơ bản, giải bài toán ta tìm được đáy lớn, đáy bé.
Trong các hình sau, hình nào là hình thang?
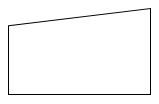
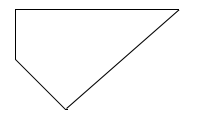
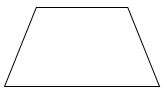
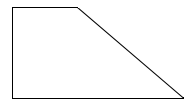
Điền số thích hợp vào ô trống:
