Câu hỏi:
1 năm trước
Đề thi THPT QG 2022 – mã đề 122
Cho hình nón có góc ở đỉnh bằng $120^o$ và chiều cao bằng 2 . Gọi $(S)$ là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của $(S)$ bằng
Trả lời bởi giáo viên
Đáp án đúng: c
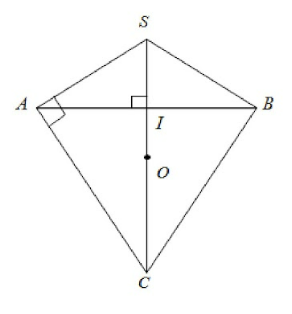
Giả sử thiết diện qua trục của hình nón là tam giác SAB với S là đỉnh hình nón và AB là đường kính đường tròn đáy.
Gọi $I$ là tâm đường tròn đáy.
\( \Rightarrow \widehat {ASB} = {120^0};SI = 2 \Rightarrow IB = 2\sqrt 3 \Rightarrow AB = 4\sqrt 3 \)
Mặt cầu chứa đường tròn đáy của hình nón thì tâm $O$ của mặt cầu thuộc đường thẳng vuông góc với mặt phẳng đáy $I$.
Mà SI luôn vuông góc với mặt phẳng đáy
=> S,O,I thẳng hàng.
=> O là điểm cách đều S, A và B
=> O là tâm đường tròn ngoại tiếp tam giác SAB.
Bán kính mặt cầu là \(R = OA = \dfrac{{AB}}{{2.\sin \widehat {ASB}}} = \dfrac{{4\sqrt 3 }}{{2.\dfrac{{\sqrt 3 }}{2}}} = 4\)
Khi đó diện tích mặt cầu là \({S_\text{cầu}} = 4\pi {R^2} = 64\pi \)
Hướng dẫn giải:
- Giả sử thiết diện qua trục của hình nón là tam giác SAB với S là đỉnh hình nón và AB là đường kính đường tròn đáy.
- Gọi $I$ là tâm đường tròn đáy.
- Chứng tỏ tâm O của mặt cầu là tâm đường tròn ngoại tiếp tam giác SAB.
- Tính bán kính đường tròn ngoại tiếp.
Câu hỏi khác
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 101 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 102 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 103 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 104 có lời giải chi tiết
- Đề thi THPT QG chính thức - 2022 - mã đề 122 có lời giải chi tiết
