Câu hỏi:
1 năm trước
Đề thi THPT QG 2022 – mã đề 122
Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\)
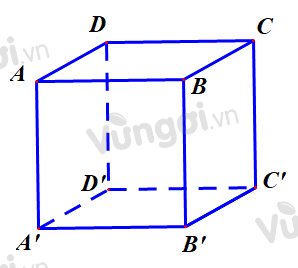
(tham khảo hình bên). Giá trị sin của góc giữa đường thẳng \(A{C^\prime }\) và mặt phẳng \((ABCD)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: b
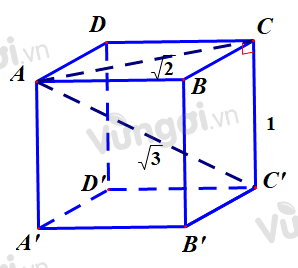
Không mất tổng quát, giả sử cạnh của hình lập phương là 1.
Khi đó \(AC = \sqrt 2 \Rightarrow AC' = \sqrt {2 + 1} = \sqrt 3 \)
Ta có: \(CC' \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {AC';\left( {ABCD} \right)} \right)}\)\( = \widehat {\left( {AC';AC} \right)} = \widehat {CAC'}\)
Ta có sin của của góc giữa đường thẳng \(A{C^\prime }\) và mặt phẳng \((ABCD)\) là \(\sin \widehat {CAC'} = \dfrac{{CC'}}{{AC'}} = \dfrac{{\sqrt 3 }}{3}\)
Hướng dẫn giải:
- Xác định hình chiếu của \(A{C’}\) trên mặt phẳng \(\left( {ABCD} \right)\): chính là \(AC\).
- Góc giữa \(A{C’}\) và \(\left( {ABCD} \right)\) là góc giữa \(A{C’}\) và \(AC\).
Câu hỏi khác
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 101 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 102 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 103 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 104 có lời giải chi tiết
- Đề thi THPT QG chính thức - 2022 - mã đề 122 có lời giải chi tiết
