Câu hỏi:
2 năm trước
Đề thi THPT QG - 2021 - mã 101
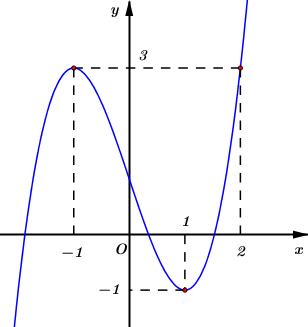
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 1\) là
Trả lời bởi giáo viên
Đáp án đúng: d
+ Để giải phương trình \(f\left( {f\left( x \right)} \right) = 1\) ta đi xét phương trình \(f\left( x \right) = 1\).
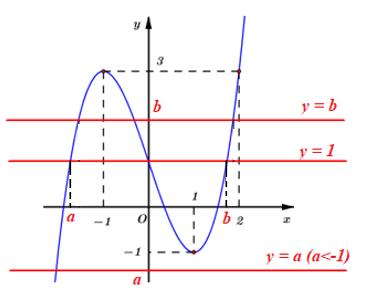
Từ đồ thị \(f\left( x \right)\) kẻ tương giao với đường thẳng \(y = 1 \Rightarrow \) Phương trình \(f\left( x \right) = 1 \Leftrightarrow \left[ \begin{array}{l}x = a\,\,\,voi\,\,a < - 1\\x = 0\\x = b\,\,voi\,\,b \in \left( {1;2} \right)\end{array} \right.\).
\( \Rightarrow \) Phương trình \(f\left( {f\left( x \right)} \right) = 1\)\( \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a \to ke\,\,tuong\,\,giao\,\,\left( {a < - 1} \right) \Rightarrow 1\,\,nghiem\\f\left( x \right) = 0 \to ke\,\,tuong\,\,giao \Rightarrow 3\,\,nghiem\\f\left( x \right) = b \to ke\,\,tuong\,\,giao\,\,b \in \left( {1;2} \right) \Rightarrow 3\,\,nghiem\end{array} \right.\)
\( \Rightarrow \) Phương trình \(f\left( {f\left( x \right)} \right) = 1\) có 7 nghiệm phân biệt.
Hướng dẫn giải:
- Giải phương trình \(f\left( x \right) = 1\) tìm \(x\) (sử dụng phương pháp tương giao đồ thị hàm số), từ đó suy ra \(f\left( x \right) = k\) nào đó.
- Tiếp tục sử dụng tương giao đồ thị hàm số giải các phương trình \(f\left( x \right) = k\) và tính tổng số nghiệm của phương trình đã cho.
Câu hỏi khác
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 101 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 102 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 103 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 104 có lời giải chi tiết
- Đề thi THPT QG chính thức - 2022 - mã đề 122 có lời giải chi tiết
