Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\), bảng biến thiên của hàm số \(f'\left( x \right)\)như sau:
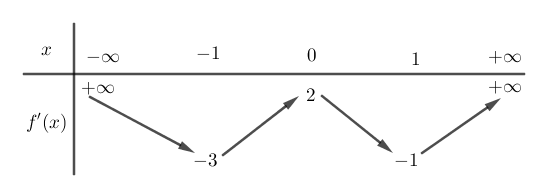
Số điểm cực trị của hàm số \(y = f\left( {4{x^2} + 4x} \right)\) là:
Trả lời bởi giáo viên
Ta có: \(y' = \left( {8x + 4} \right)f'\left( {4{x^2} + 4x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\f'\left( {4{x^2} + 4x} \right) = 0\end{array} \right.\).
\(f'\left( {4{x^2} + 4x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}4{x^2} + 4x = {x_1}\,\,\left( {{x_1} < - 1} \right)\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\4{x^2} + 4x = {x_2}\,\,\left( { - 1 < {x_2} < 0} \right)\,\,\left( 2 \right)\\4{x^2} + 4x = {x_3}\,\,\left( {0 < {x_3} < 1} \right)\,\,\,\,\,\,\left( 3 \right)\\4{x^2} + 4x = {x_4}\,\,\left( {1 < {x_4}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\end{array} \right.\)
Xét phương trình \(4{x^2} + 4x = {x_i} \Leftrightarrow 4{x^2} + 4x - {x_i} = 0\,\,\left( * \right)\) ta có: \(\Delta ' = 4 + 4{x_i}\).
+) \(\Delta ' < 0 \Leftrightarrow 4 + 4{x_i} < 0 \Leftrightarrow {x_i} < - 1 \Rightarrow \) Phương trình vô nghiệm.
+) \(\Delta ' = 0 \Leftrightarrow {x_i} = - 1 \Rightarrow \) Phương trình có nghiệm kép \(x = - \dfrac{1}{2}\).
+) \(\Delta ' > 0 \Leftrightarrow {x_i} > - 1 \Rightarrow \) Phương trình có 2 nghiệm phân biệt \(x \ne - \dfrac{1}{2}\).
Do đó:
Phương trình (1) vô nghiệm.
Phương trình (2, (3), (4) có 2 nghiệm phân biệt \(x \ne - \dfrac{1}{2}\).
Vậy phương trình \(y' = 0\) có 7 nghiệm đơn phân biệt hay hàm số \(y = f\left( {4{x^2} + 4x} \right)\) có 7 cực trị.
Hướng dẫn giải:
- Giải phương trình \(f'\left( u \right) = 0\) với \(u = 4{x^2} + 4x\)
- Xét các phương trình \(4{x^2} + 4x = a\)

