Đề thi THPT QG 2019 – mã đề 104

Cho hàm số bậc ba \(y = f\left( x \right)\)có đồ thị như hình vẽ bên.

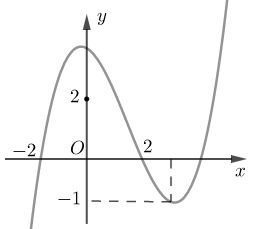
Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{2}{3}\) là

\(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{2}{3} \Leftrightarrow \left[ \begin{array}{l}f\left( {{x^3} - 3x} \right) = \dfrac{2}{3}\,\,\,\,\,\,\left( * \right)\\f\left( {{x^3} - 3x} \right) =  - \dfrac{2}{3}\,\,\left( {**} \right)\end{array} \right.\)

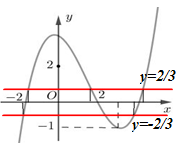
\(Pt\left( * \right) \Leftrightarrow \left[ \begin{array}{l}{x^3} - 3x = {x_1}\,\,\left( { - 2 < {x_1} < 0} \right)\,\,\left( 1 \right)\\{x^3} - 3x = {x_2}\,\,\left( {0 < {x_2} < 2} \right)\,\,\,\,\left( 2 \right)\\{x^3} - 3x = {x_3}\,\,\left( {{x_3} > 2} \right)\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)

\(Pt\left( {**} \right) \Leftrightarrow \left[ \begin{array}{l}{x^3} - 3x = {x_4}\,\,\left( {{x_4} <  - 2} \right)\,\,\,\,\left( 4 \right)\\{x^3} - 3x = {x_5}\,\,\left( {{x_5} > 2} \right)\,\,\,\,\,\,\,\left( 5 \right)\\{x^3} - 3x = {x_6}\,\,\left( {{x_6} > 2} \right)\,\,\,\,\,\,\,\left( 6 \right)\end{array} \right.\)

Xét phương trình \(g\left( x \right) = {x^3} - 3x = {x_i}\), số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = g\left( x \right)\) và đường thẳng \(y = {x_i}\) song song với trục hoành.

Ta có \(g'\left( x \right) = 3{x^2} - 3 = 0 \Leftrightarrow x =  \pm 1\).

BBT:

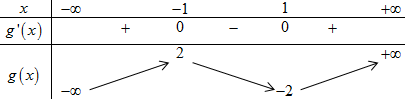
Từ BBT ta thấy:

(1), (2) có 3 nghiệm phân biệt.

(3), (4), (5), (6) có 1 nghiệm.

Và dễ thấy tất cả các nghiệm trên là không trùng nhau.

Vậy phương trình ban đầu có 10 nghiệm phân biệt.